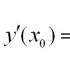乗算の導関数。導関数を見つける：アルゴリズムとソリューションの例

導関数とその計算方法の知識がなければ、数学の物理的な問題や例を解決することは絶対に不可能です。微分は、数学的分析の最も重要な概念の1つです。今日の記事をこの基本的なトピックに捧げることにしました。導関数とは何ですか、その物理的および幾何学的意味は何ですか、関数の導関数を計算する方法は何ですか？これらすべての質問を1つにまとめることができます：導関数を理解する方法は？

導関数の幾何学的および物理的意味

機能があるようにしましょう f（x） 一定の間隔で与えられる （a、b） ..。ポイントхとх0はこの区間に属します。 xが変わると、関数自体も変わります。引数の変更-その値の違い x-x0 ..。この違いは次のように書かれています デルタx 引数の増分と呼ばれます。関数の変更または増分は、2つのポイントでの関数の値の差です。派生的な定義：

ある点での関数の導関数は、引数がゼロになる傾向がある場合の、引数の増分に対する特定の点での関数の増分の比率の限界です。

それ以外の場合は、次のように記述できます。

そのような限界を見つけることのポイントは何ですか？そして、これが何です：

ある点での関数の導関数は、OX軸間の角度の接線とこの点での関数のグラフの接線に等しくなります。

派生物の物理的意味： 時間に関する経路の導関数は、直線運動の速度に等しくなります。

確かに、学校時代から、誰もがスピードが私的な道であることを知っています。 x = f（t） と時間 NS ..。一定期間の平均速度：

一度に移動速度を調べるには t0 制限を計算する必要があります：

ルール1：定数を取り出す

定数は導関数の符号の外側に移動できます。さらに、それは行われなければなりません。数学で例を解くときは、原則として- 式を単純化できる場合は、必ず単純化してください .

例。導関数を計算してみましょう：

ルール2：関数の合計の導関数

2つの関数の合計の導関数は、これらの関数の導関数の合計に等しくなります。関数の違いの導関数についても同じことが言えます。

この定理の証明はしませんが、実際的な例を考えます。

関数の導関数を見つけます。

ルール3：関数の積の導関数

2つの微分可能関数の積の導関数は、次の式で計算されます。

例：関数の導関数を見つける：

解決：

ここで、複素関数の導関数の計算について言うことが重要です。複素関数の導関数は、独立変数に関する中間引数の導関数による、中間引数に関するこの関数の導関数の積に等しくなります。

上記の例では、次の式が満たされています。

この場合、中間引数は8の5乗です。このような式の導関数を計算するために、最初に中間引数に関する外部関数の導関数を計算し、次に独立変数に関する直接の中間引数の導関数を乗算します。

ルール4：2つの関数の商導関数

2つの関数の商の導関数を決定するための式：

ダミーのデリバティブを一からお伝えしようと思いました。このトピックは思ったほど単純ではないので、注意してください。例には落とし穴があることが多いので、導関数を計算するときは注意してください。

このトピックやその他のトピックに関する質問については、学生サービスにお問い合わせください。これまで導関数の計算を行ったことがない場合でも、短時間で、最も困難なテストの解決とタスクの処理を支援します。

関数とを点のある近傍で定義し、その点に導関数を持たせます。次に、それらの製品は、次の式によって決定されるポイントに導関数を持ちます。
(1) .

証拠

表記法を紹介しましょう：
;
.
ここにとは変数との関数です。ただし、簡単にするために、引数の表記は省略します。

さらに、注意してください
;
.
条件により、関数とはある点で導関数を持ちます。これは次の制限です。
;
.
導関数の存在は、関数とがその点で連続であることを意味します。したがって
;
.

関数と次の積である変数xの関数yについて考えてみます。
.
ある時点でのこの関数の増分について考えてみます。

.
今、私たちは導関数を見つけます：

.

それで、
.
ルールは証明されています。

変数の代わりに他の変数を使用できます。それをxと表記しましょう。次に、導関数とがある場合、2つの関数の積の導関数は次の式で決定されます。
.
またはより短い記録で
(1) .

結果

独立変数xの関数とします。それで
;
;
NS。 ...

最初の式を証明しましょう。最初に、関数とに積（1）の導関数の式を適用し、次に関数とに-を適用します。

.

他の同様の公式も同様に証明されています。

の例

例1

導関数を見つける
.

2つの関数の積の微分法則を適用します
(1) .
.

導関数の表から、次のことがわかります。
;
.
それで
.

最後に、次のようになります。
.

例2

変数xの関数の導関数を見つけます
.

2つの関数の積の導関数の式を適用します。
(1) .
.

和の導関数と関数の差の式を適用します。
.
.

定数を区別するためのルールを適用します。
;
.
;
.

と トピック「デリバティブ」に関する参考資料。基本的な学校レベル。
数学の学生、教師、家庭教師のための理論的情報。クラスの実施を支援するため。

意味：ある点での関数の導関数は、変数の増分に対する関数の増分の比率の限界です。

基本的な数学関数の微分表：

微分計算規則

金額の導関数任意の2つの式は、これらの式の導関数の合計に等しくなります（合計の導関数は導関数の合計に等しくなります）

違いの派生物任意の2つの式は、これらの項の導関数の差に等しくなります（差の導関数は導関数の差に等しくなります）。

作品の派生物 2つの因子の積は、最初の因子の2番目の導関数と2番目の因子の導関数の積（順番に取られた因子の導関数の合計）に等しくなります。
数学の家庭教師のコメント：製品の導関数を計算するための規則について短いフレーズで学生に思い出させるとき、私はこれを言います：2番目のプラスによる最初の因子の導関数 ストロークの交換！

商から派生 2つの式は、因子の導関数の差の商と分母の2乗に等しくなります。

関数による数の積の導関数..。数値とリテラル式（関数による）の積の導関数を見つけるには、この数値にこのリテラル式の導関数を掛ける必要があります。

複雑な関数の導関数：

複素関数の導関数を計算するには、外側の関数の導関数を見つけて、それを内側の関数の導関数で乗算する必要があります。

デリバティブページでのコメントとフィードバック：
アレクサンダーS。
テーブルはとても必要でした。インターネット上では、最も多いものの1つです。説明とルールをありがとうございました。彼らへの少なくとももう一つの例、そして一般的にそれは素晴らしいでしょう。再度、感謝します。

Kolpakov A.N.、数学の家庭教師： OK、近い将来、いくつかの例をページに追加しようと思います。

仮想数学参考書。
コルパコフアレクサンドルニコラエヴィッチ、数学の家庭教師。

覚えるのはとても簡単です。

さて、遠くまで行かないで、すぐに逆関数を検討します。指数関数の逆関数はどれですか？対数：

私たちの場合、ベースは数値です。

このような対数（つまり、底を持つ対数）は「自然」と呼ばれ、そのために特別な表記法を使用します。代わりに記述します。

とは何ですか？もちろん、。

自然対数の導関数も非常に単純です。

例：

関数の導関数を見つけます。
関数の導関数は何ですか？

回答： 指数と自然対数は、導関数の観点からは一意に単純な関数です。他のベースを使用した指数関数と対数関数は、微分の規則を通過した後、後で分析する異なる導関数を持ちます。

微分法則

何のルール？再び新しい用語、再び？！..。

差別化導関数を見つけるプロセスです。

それで全部です。このプロセスを一言で呼ぶ他の方法はありますか？派生ではありません...数学の微分は、関数の同じ増分と呼ばれます。この用語はラテン語の差異、つまり差異に由来します。ここに。

これらすべてのルールを導出するときは、たとえば、、の2つの関数を使用します。また、増分の式も必要です。

全部で5つのルールがあります。

定数は微分記号の外側に移動します。

が定数（定数）の場合、。

明らかに、このルールは違いに対しても機能します。

それを証明しましょう。しましょう、またはもっと簡単に。

例。

関数の導関数を見つけます。

その時点で;
その時点で;
その時点で;
その時点で。

ソリューション：

（導関数は線形関数であるため、すべての点で同じです、覚えていますか？）;

作品の派生物

ここではすべて同じです。新しい関数を導入し、その増分を見つけます。

派生物：

例：

関数の導関数を見つけて;
その点で関数の導関数を見つけます。

ソリューション：

指数関数の導関数

これで、指数だけでなく、指数関数の導関数を見つける方法を学ぶのに十分な知識があります（それが何であるかを忘れましたか？）。

だから、どこにいくつかの数字があります。

関数の導関数はすでにわかっているので、関数を新しい基数にキャストしてみましょう。

これを行うには、次の簡単なルールを使用します。それで：

まあ、それはうまくいきました。ここで導関数を見つけてみてください。この関数には注意が必要です。

起こりました？

ここで、自分自身を確認してください。

数式は指数の導関数に非常に似ていることが判明しました。それはそのままで、乗数のみが表示されました。これは単なる数値であり、変数ではありません。

例：
関数の導関数を見つけます。

回答：

これは、電卓なしでは計算できない数値です。つまり、より単純な形式で記述することはできません。したがって、回答ではこの形式のままにしておきます。

これが2つの関数の商であるため、対応する微分法則を適用することに注意してください。

この例では、2つの関数の積です。

対数関数の導関数

ここでも同様です。自然対数の導関数をすでに知っています。

したがって、異なる底を持つ対数の任意の1つを見つけるには、たとえば次のようにします。

この対数を底辺に持ってくる必要があります。対数の底をどのように変更しますか？この式を覚えておいてください。

今だけ代わりに書きます：

分母は単なる定数です（定数、変数なし）。導関数は非常に単純です。

指数関数と対数関数の導関数がUSEで見つかることはほとんどありませんが、それらを知ることは不必要ではありません。

複雑な関数の導関数。

「複雑な機能」とは何ですか？いいえ、これは対数ではなく、逆正接でもありません。これらの関数は理解するのが難しい場合がありますが（対数が難しいと思われる場合は、トピック「対数」を読んですべてが通過します）、数学の観点から、「難しい」という言葉は「難しい」を意味しません。

小さなコンベヤーベルトを想像してみてください。2人が座って、いくつかのオブジェクトを使って何らかのアクションを実行しています。たとえば、1つ目はチョコレートバーをラッパーで包み、2つ目はリボンで結びます。それはそのような複合オブジェクトであることがわかります：リボンで包まれて結ばれたチョコレートバー。チョコレートバーを食べるには、逆の手順を逆の順序で行う必要があります。

同様の数学的パイプラインを作成しましょう。最初に数値の余弦を見つけ、次に結果の数値を2乗します。だから、私たちは番号（チョコレートバー）を与えられ、私はそのコサイン（ラッパー）を見つけ、そしてあなたは私が得たものを二乗します（あなたはそれをリボンで結びます）。どうしたの？関数。これは複雑な関数の例です。その値を見つけるために、変数を使用して最初のアクションを直接実行し、次に最初のアクションの結果を使用して別の2番目のアクションを実行する場合。

言い換えると、複素関数は、引数が別の関数である関数です。: .

この例では、。

同じアクションを逆の順序で実行することもできます。最初に2乗し、次に結果の数値の余弦を探します。結果はほとんど常に異なると推測するのは簡単です。複雑な関数の重要な機能：アクションの順序を変更すると、関数が変更されます。

2番目の例:(同じ）。 ..。

最後に行うアクションは呼び出されます 「外部」機能、および最初に実行されるアクション-それぞれ 「内部」機能（これらは非公式の名前であり、私はそれらを簡単な言葉で資料を説明するためにのみ使用します）。

どの機能が外部でどれが内部であるかを自分で判断してみてください。

回答：内部関数と外部関数の分離は、変数の変更と非常によく似ています。たとえば、関数内です。

最初に取るべき行動は何ですか？最初に正弦を計算し、次にそれを立方体に上げます。これは、それが内部機能であるが、外部機能であることを意味します。
そして、元の機能はそれらの構成です：。
内部：; 外部の：。
審査：。
内部：; 外部の：。
審査：。
内部：; 外部の：。
審査：。
内部：; 外部の：。
審査：。

変数を変更して関数を取得します。

さて、今度はチョコレートバーを抽出します-派生物を探します。手順は常に逆になります。最初に外部関数の導関数を探し、次に結果に内部関数の導関数を掛けます。元の例に関連して、次のようになります。

もう一つの例：

それでは、最終的に公式ルールを策定しましょう。

複素関数の導関数を見つけるためのアルゴリズム：

すべてが単純なようですよね？

例で確認しましょう：

ソリューション：

1）内部：;

外部の：;

2）内部：;

（今ではカットしようとしないでください！コサインの下から何も取り出せません、覚えていますか？）

3）内部：;

外部の：;

ここに3レベルの複雑な関数があることはすぐにわかります。結局のところ、これはそれ自体がすでに複雑な関数であり、そこからルートを抽出します。つまり、3番目のアクションを実行します（チョコレートを入れます）ラッパーとポートフォリオ内のリボン付き）。しかし、恐れる理由はありません。それでも、この関数を通常と同じ順序で「解凍」します。最後からです。

つまり、最初にルートを区別し、次にコサインを区別し、次に括弧内の式のみを区別します。そして、これをすべて乗算します。

このような場合、アクションに番号を付けると便利です。つまり、私たちが知っていることを想像してみましょう。この式の値を計算するアクションをどのような順序で実行しますか？例を見てみましょう：

アクションが後で実行されるほど、対応する機能はより「外部」になります。アクションのシーケンス-以前と同じように：

ここでは、ネストは通常4レベルです。行動方針を定義しましょう。

1.過激な表現。 ..。

2.ルート。 ..。

3.副鼻腔。 ..。

4.正方形。 ..。

5.すべてをまとめる：

デリバティブ。メインについて簡単に

関数の導関数-無限に小さい引数増分での引数増分に対する関数増分の比率：

基本的な導関数：

微分法則：

定数は微分記号の外側に移動します。

金額の導関数：

作品の派生物：

商の導関数：

複雑な関数の導関数：

複素関数の導関数を見つけるためのアルゴリズム：

「内部」関数を定義し、その導関数を見つけます。
「外部」関数を定義し、その導関数を見つけます。
1点目と2点目の結果を掛けます。

定義に従うと、ある点での関数の導関数は、関数の増分の比率の限界Δです。 y引数Δの増分に NS:

すべてが明確なようです。しかし、この式、たとえば関数の導関数を使用して計算してみてください NS(NS) = NS 2 + (2NS+ 3） e NS罪 NS..。定義上すべてを行う場合、数ページの計算の後、あなたはただ眠りに落ちるでしょう。したがって、より簡単で効果的な方法があります。

まず、いわゆる初等関数は、さまざまな関数と区別できることに注意してください。これらは比較的単純な式であり、その導関数は長い間計算されてテーブルに入力されてきました。そのような関数は、それらの導関数とともに、覚えるのに十分簡単です。

初等関数の導関数

初等関数は以下のすべてです。これらの関数の派生物を心から知る必要があります。さらに、それらを暗記することはまったく難しいことではありません-それが彼らが初歩的である理由です。

したがって、初等関数の導関数は次のとおりです。

名前	関数	デリバティブ
絶え間ない	NS(NS) = NS, NS ∈ NS	0（はい、ゼロです！）
有理グレード	NS(NS) = NS NS	NS · NS NS − 1
副鼻腔	NS(NS）=罪 NS	cos NS
余弦	NS(NS）= cos NS	-罪 NS（マイナスサイン）
正接	NS(NS）= tg NS	1 / cos 2 NS
コタンジェント	NS(NS）= ctg NS	--1 / sin 2 NS
自然対数	NS(NS）= ln NS	1/NS
任意の対数	NS(NS）=ログ NS NS	1/(NS Ln NS)
指数関数	NS(NS) = e NS	e NS（何も変わっていません）

初等関数に任意の定数を掛けると、新しい関数の導関数も簡単に計算できます。

(NS · NS)’ = NS · NS ’.

一般に、定数は導関数の符号の外側に移動できます。例えば：

(2NS 3） ’= 2・（ NS 3） '= 2 3 NS 2 = 6NS 2 .

明らかに、初等関数は互いに加算したり、乗算したり、分割したりすることができます。したがって、新しい関数が表示されます。これは、特に基本的なものではありませんが、特定のルールに従って微分可能です。これらのルールについては、以下で説明します。

和と差の導関数

関数をしましょう NS(NS）と NS(NS）、その派生物は私たちに知られています。たとえば、上記の初等関数を使用できます。次に、これらの関数の合計と差の導関数を見つけることができます。

(NS + NS)’ = NS ’ + NS ’
(NS − NS)’ = NS ’ − NS ’

したがって、2つの関数の合計（差）の導関数は、導関数の合計（差）に等しくなります。もっと用語があるかもしれません。例えば、（ NS + NS + NS)’ = NS ’ + NS ’ + NS ’.

厳密に言えば、代数には「引き算」の概念はありません。「ネガティブエレメント」という概念があります。したがって、違い NS − NS合計として書き換えることができます NS+（-1） NS、そして1つの式だけが残ります-合計の導関数。

NS(NS) = NS 2 + sin x; NS(NS) = NS 4 + 2NS 2 − 3.

関数 NS(NS）は、2つの初等関数の合計であるため、次のようになります。

NS ’(NS) = (NS 2+罪 NS)’ = (NS 2） ’+（sin NS)’ = 2NS+ cos x;

関数についても同様に議論します NS(NS）。（代数の観点から）すでに3つの用語があるだけです：

NS ’(NS) = (NS 4 + 2NS 2 − 3)’ = (NS 4 + 2NS 2 + (−3))’ = (NS 4)’ + (2NS 2)’ + (−3)’ = 4NS 3 + 4NS + 0 = 4NS · ( NS 2 + 1).

答え：
NS ’(NS) = 2NS+ cos x;
NS ’(NS) = 4NS · ( NS 2 + 1).

作品の派生物

数学は論理科学であるため、合計の導関数が導関数の合計と等しい場合、積の導関数はストライク">は導関数の積に等しい。しかし、あなたを想像してみてください！積の導関数は、まったく異なる式を使用して計算されます。つまり、次のようになります。

(NS · NS) ’ = NS ’ · NS + NS · NS ’

式は単純ですが、見過ごされがちです。そして、学童だけでなく、学生も。結果は誤って解決された問題です。

仕事。関数の導関数を見つける： NS(NS) = NS 3 cos x; NS(NS) = (NS 2 + 7NS- 7） e NS .

関数 NS(NS）は2つの初等関数の積であるため、すべてが単純です。

NS ’(NS) = (NS 3 cos NS)’ = (NS 3） ’cos NS + NS 3（cos NS)’ = 3NS 2 cos NS + NS 3（-sin NS) = NS 2（3cos NS − NS罪 NS)

関数 NS(NS）最初の要素はもう少し複雑ですが、一般的なスキームはこれから変わりません。明らかに、関数の最初の要素 NS(NS）は多項式であり、その導関数は合計の導関数です。我々は持っています：

NS ’(NS) = ((NS 2 + 7NS- 7） e NS)’ = (NS 2 + 7NS- 7） ' e NS + (NS 2 + 7NS- 7）（ e NS)’ = (2NS+ 7） e NS + (NS 2 + 7NS- 7） e NS = e NS・（2 NS + 7 + NS 2 + 7NS −7) = (NS 2 + 9NS) · e NS = NS(NS+ 9） e NS .

答え：
NS ’(NS) = NS 2（3cos NS − NS罪 NS);
NS ’(NS) = NS(NS+ 9） e NS .

最後のステップで、導関数が因数分解されることに注意してください。正式には、これを行う必要はありませんが、ほとんどの導関数はそれ自体では計算されませんが、関数を調査するために計算されます。これは、さらに導関数がゼロに等しくなり、その符号が明確になることなどを意味します。このような場合は、因数分解された式を使用することをお勧めします。

2つの機能がある場合 NS(NS）と NS(NS）、と NS(NS）≠0関心のあるセットで、新しい関数を定義できます NS(NS) = NS(NS)/NS(NS）。このような関数については、導関数を見つけることもできます。

弱くないですよね？マイナスはどこから来たのですか？どうして NS 2？そうです！これは最も難しい式の1つです-ボトルなしではそれを理解することはできません。したがって、具体的な例を挙げて検討することをお勧めします。

仕事。関数の導関数を見つける：

各分数の分子と分母には初等関数が含まれているため、必要なのは商の導関数の式だけです。

伝統的に、分子を因数分解すると、答えが大幅に単純化されます。

複雑な関数は、必ずしも0.5kmの長さの式である必要はありません。たとえば、関数を取るだけで十分です NS(NS）=罪 NS変数を置き換えます NSと言いましょう NS 2 + ln NS..。それが判明します NS(NS）=罪（ NS 2 + ln NS）は複雑な関数です。派生物もありますが、上記のルールに従ってそれを見つけることはできません。

どうなる？このような場合、変数の置換と複素関数の導関数の式は次のことに役立ちます。

NS ’(NS) = NS ’(NS) · NS'、もしも NSに置き換えられます NS(NS).

原則として、この式を理解すると、商の導関数よりも状況はさらに悲しくなります。したがって、各ステップの詳細な説明とともに、具体的な例で説明することもお勧めします。

仕事。関数の導関数を見つける： NS(NS) = e 2NS + 3 ; NS(NS）=罪（ NS 2 + ln NS)

関数内の場合は注意してください NS(NS）式2の代わりに NS+3は簡単になります NS、次に初等関数を取得します NS(NS) = e NS..。したがって、置換を行います。let2 NS + 3 = NS, NS(NS) = NS(NS) = e NS..。次の式で複素関数の導関数を探しています。