微分によるシンプレックス法のオンラインソリューション。 シンプレックス法によるzlpの解法
LP問題を解くための普遍的な方法は、シンプレックス法と呼ばれます。 この方法の適用とその最も一般的な変更-2フェーズシンプレックス法。
LP問題を解くためのグラフィカルな方法では、目的関数の値が最大(最小)に達した頂点など、不等式のシステムの解のセットの境界に属する頂点のセットから実際に選択しました。 2つの変数の場合、この方法は非常に明確であり、問題の解決策をすばやく見つけることができます。
問題に3つ以上の変数があり、これが実際の経済問題の状況である場合、制約システムのソリューションの領域を視覚化することは困難です。 そのようなタスクはの助けを借りて解決されます シンプレックス法 または継続的な改善の方法。 この方法の考え方は単純で、次のように構成されています。
ある規則に従って、初期参照計画(制約領域の頂点)が見つかります。 計画が最適かどうかをチェックします。 はいの場合、問題は解決されています。 そうでない場合は、別の改善された計画、つまり別の頂点に移動します。 この計画(この頂点で)の目的関数の値は、前の計画よりも確かに優れています。 遷移アルゴリズムは、いくつかの計算ステップの助けを借りて実行されます。これは、次のようなテーブルの形式で便利に記述されています。 シンプレックステーブル 。 頂点の数は有限であるため、有限のステップ数で最適なソリューションに到達します。
計画を立てるタスクの特定の例でシンプレックス法を考えてみましょう。
繰り返しになりますが、シンプレックス法は、特殊な形式に縮小された正規LP問題の解決に適用できることに注意してください。つまり、基底、正の右辺、および非基底変数で表される目的関数を持ちます。 問題が特別な形に還元されない場合は、追加の手順が必要です。これについては後で説明します。
以前にモデルを作成し、それを特別な形に縮小した生産計画の問題を考えてみましょう。
仕事。
製品の製造のため Aと V倉庫は80ユニット以下の原材料をリリースできます。 そして製品の製造のために A 2ユニットが消費され、製品 V-原材料の1単位。 製品が最大の利益を確実にするように生産を計画する必要があります A 50個以下の生産が必要であり、製品 V-40個以下。 さらに、1つの製品の販売からの利益 A-5ルーブル、およびから V-3回こすります。
数学モデルを構築してみましょう。 バツ 1製品Aの数 バツ 2-製品の数 V。 その場合、制約システムは次のようになります。
x1≤50
x2≤40
2x1 +x2≤80
x1≥0、x2≥0
5x1 + 3x2→max
追加の変数を導入することにより、問題を標準形にします。
x 1 + x 3 = 50
x2 + x4 = 40
2x1 + x2 + x5 = 80
x1≥0、x2≥0
5x1 + 3x2→max
-F = -5x 1-3x2→最小。
この問題には特別な形式があります(基本的に、右側は負ではありません)。 シンプレックス法で解くことができます。
私ステージ。シンプレックステーブルへのタスクの書き込み。 問題の制約システム(3.10)とシンプレックスタブローの間には1対1の対応があります。 テーブルには、制約システムの等式と同じ数の行と、自由変数と同じ数の列があります。 基本変数は最初の列を埋め、自由変数はテーブルの一番上の行を埋めます。 一番下の行はインデックスラインと呼ばれ、目的関数の変数の係数が含まれています。 関数に空きメンバーがない場合、右下隅に最初に0が書き込まれます。 ある場合は、反対の符号で書き込みます。 この場所(右下隅)には、目的関数の値があります。これは、あるテーブルから別のテーブルに移動するときにモジュロを増加させる必要があります。 したがって、制限のシステムは表3.4に対応しており、ソリューションの第2段階に進むことができます。
表3.4
|
基本 |
自由 |
||
IIステージ。 基本計画の最適性を確認します。
この表3.4は、次のベースラインに対応しています。
(バツ 1 , バツ 2 , バツ 3 , バツ 4 , バツ 5) = (0, 0, 50, 40, 80).
自由変数 バツ 1 , バツ 2は0です。 バツ 1 = 0, バツ 2 = 0。そして基本変数 バツ 3 , バツ 4 , バツ 5値を取る バツ 3 = 50, バツ 4 = 40, バツ 5 = 80-無料メンバーの列から。 目的関数値:
-F = - 5バツ 1 - 3バツ 2 = -5 0-3 0 = 0。
私たちの仕事は、与えられた基本計画が最適であるかどうかを確認することです。 これを行うには、インデックスライン(目的関数のライン)を確認する必要があります F.
さまざまな状況が考えられます。
1.インデックス内 F-文字列には負の要素はありません。 したがって、計画は最適であり、問題の解決策を書き出すことができます。 ターゲット関数は、反対の符号で取得された、右下隅の数値に等しい最適値に達しました。 ステージIVに移りましょう。
2.インデックス行に少なくとも1つの負の要素があり、その列には正の要素がありません。 次に、目的関数は F→∞は無期限に減少します。
3.インデックス行に負の要素があり、その列には少なくとも1つの正の要素が含まれています。 次に、次のステージIIIに進みます。 テーブルを再計算して、ベースラインを改善します。
IIIステージ。 基本計画の改善。
インデックスの負の要素の F-最大のモジュロを選択する行。それに対応する列を解決と呼び、「」とマークします。
解決する行を選択するには、フリーメンバーの列の要素の比率を計算する必要があります それだけに ポジティブ権限列要素。 得られた比率から最小値を選択します。 最小値に達する対応する要素は、解決要素と呼ばれます。 四角で強調表示します。
この例では、要素2は許容されます。 この要素に対応する文字列は、解決とも呼ばれます(表3.5)。
表3.5

解決要素を選択したら、次のルールに従ってテーブルを再計算します。
1.以前と同じサイズの新しいテーブルで、解決する行変数と列変数が交換されます。これは、新しい基底への遷移に対応します。 この例では: バツ代わりに1がベースに含まれます バツ 5、これは基礎を離れ、現在は無料です(表3.6)。
表3.6
2.分解要素2の代わりに、その逆数½を書き込みます。
3.許容線の要素を許容要素で割ります。
4.解決列の要素は、解決要素によって分割され、反対の符号で書き込まれます。
5.表3.6の残りの要素を入力するために、長方形のルールに従って再計算します。 50の場所にある要素を数えたいとしましょう。
この要素を解決する要素と精神的に結び付け、積を見つけ、結果の長方形のもう一方の対角線上にある要素の積を減算します。 差は解決要素で除算されます。
そう、 。 50だったところに10と書きます。同様に:
, ![]() , ,
, , ![]() .
.
表3.7

新しいテーブル3.7があり、基本変数は変数(x 3、x 4、x 1)になりました。 目的関数の値は-200に等しくなりました。 減少しました。 この基本的なソリューションの最適性を確認するには、ステージIIに戻る必要があります。 プロセスは明らかに有限であり、停止基準はステージIIのポイント1と2です。
問題の解決策を完成させましょう。 これを行うには、インデックス行をチェックし、その中に負の要素-½が含まれていることを確認して、それに対応する列を解決するように呼び出し、ステージIIIに従ってテーブルを再計算します。 比率を作成し、その中から最小値= 40を選択したので、解決要素1を決定しました。次に、ルール2〜5に従って再計算が実行されます。
表3.8
テーブルを再計算した後、インデックス行に負の要素がないことを確認します。したがって、問題は解決され、基本計画が最適になります。
IVステージ。 最適なソリューションを書き出す。
ステージIIのポイント1に従ってシンプレックス法が停止した場合、問題の解決策は次のように書き出されます。 基本変数は、それぞれ無料メンバーの列の値を取ります。 この例では バツ 3 = 30, バツ 2 = 40, バツ 1 = 20。自由変数は0、 バツ 5 = 0, バツ 4 = 0。目的関数は、反対の符号を持つ自由項の列の最後の要素の値を取ります。- F = -220 → F= 220、この例では、関数は最小で、最初は検査されました F→maxなので、実際には2回符号が変わりました。 そう、 バツ* = (20, 40, 30, 0, 0), F* = 220。問題への回答:
このタイプの製品を20個リリース計画に含める必要があります A、タイプBの40の製品、利益は最大で220ルーブルに相当します。
このセクションの最後に、手順を正確に繰り返すシンプレックス法アルゴリズムのフローチャートを示しますが、矢印が明確なアクションの方向を示しているため、読者によっては使用する方が便利な場合があります。
フローチャートのボックスの上のリンクは、対応する変換グループが属するステップまたはサブアイテムを示しています。 初期ベースラインを見つけるためのルールは、3.7項で定式化されます。

例。 シンプレックス法を使用して、次のLP問題を標準形で解きます。
f(x)= x 1 + 9x 2 + 5x 3 + 3x 4 + 4x 5 + 14x6→分
x1 + x4 = 20
x2 + x5 = 50
x 3 + x 6 = 30
x 4 + x 5 + x 6 = 60
xi≥0、i = 1、…、6
LP問題は、すべての制約(変数の非負性の条件を除く)が等式であり、すべての自由項が非負である場合、標準形であると言われます。 したがって、標準形の問題があります。
シンプレックス法の考え方は次のとおりです。 最初に、許容可能な解(初期の許容可能な基本解)の多面体のいくつかの(初期)頂点を見つける必要があります。 次に、このソリューションの最適性を確認する必要があります。 それが最適である場合、解決策が見つかります。 そうでない場合は、多面体の別の頂点に移動して、最適性を再度確認します。 多面体の頂点の有限性(LP問題の制限の有限性の結果)を考慮して、有限数の「ステップ」で、目的の最小点または最大点を見つけます。 ある頂点から別の頂点に移動すると、目的関数の値が減少する(最小の問題の場合)か増加する(最大の問題の場合)ことに注意してください。
したがって、シンプレックス法のアイデアは、LP問題の3つの特性に基づいています。
解決。最初の実行可能な基本的な解決策を見つけるために、すなわち。 基本変数を決定するには、システム(5.6)を「対角」形式に縮小する必要があります。 ガウスの方法(未知数を連続的に除去する方法)を適用すると、(5.6)から次のようになります。
x 2 + x 1 + x 3 \ u003d 40
x4 + x1 = 20
x5 -x1 -x3 = 10
x6 + x3 = 30
したがって、変数は基本的なものです x 2、x 4、x 5、x 6、対応する行の無料メンバーに等しい値をそれらに与えます: x 2 \ u003d 40、x 4 \ u003d 20、x 5 \ u003d 10、x 6 \ u003d 30。 変数 x 1と x 3非基本的です: x 1 \ u003d 0、x 3 \ u003d 0.
最初に許容される基本的なソリューションを構築しましょう
x 0 =(0.40,0.20,10.30)(5.9)
見つかったソリューションの最適性を確認するには x0(システム(5.8)の助けを借りて)目的関数から基本変数を除外し、特別なシンプレックステーブルを作成する必要があります。
変数を削除した後、目的関数を次の形式で記述すると便利です。
f(x)= -7x 1-14x 3 +880(5.10)
ここで、(5.8)-(5.10)を使用して、初期シンプレックステーブルを作成します。 
ゼロラインには、目的関数の対応する変数の符号が反対の係数が含まれています。 最適性基準(最小探索問題の場合):許容される基本的な解決策( x0)は、ゼロ行に厳密に正の数が1つもない場合に最適です(目的関数(880)の値はカウントされません)。 このルールは、次の反復(テーブル)にも適用されます。 ゼロ行の要素は、列推定と呼ばれます。
したがって、最初に許容される基本的なソリューション(5.9)は最適ではありません。 7>0, 14>0
.
ゼロ列には、基本変数の値が含まれています。 それらは必然的に非負でなければなりません(式(5.7)を参照)。 1行目から4行目まで、システム(5.8)の変数の係数が書き込まれます。
なぜなら x0が最適ではない場合は、許容される解の多面体の別の頂点に移動する必要があります(新しいd.b.r.を作成します)。 これを行うには、主要な要素を見つけて、特定の変換(シンプレックス変換)を実行する必要があります。
最初に、テーブルの先頭の要素を見つけます。これは、先頭の列(正のスコアが最も高い列)と先頭の行(ゼロ列の要素の最小比率に対応する行)の交点にあります。先頭の列の対応する要素(厳密に正))。
表1では、先頭の列が3番目の列であり、先頭の行が4番目の行です。 (min(40 / 1,30 / 1)= 30/1)は矢印で示され、先頭の要素は丸で囲まれています。 先頭の要素は、基本変数が x6非基本的なものと交換する必要があります x 3。 次に、新しい基本変数は次のようになります x 2、x 3、x 4、x 5、、および非基本- x 1、x 6、。 これは、許容される解の多面体の新しい頂点への遷移を意味します。 新しい実行可能な基本ソリューションの座標値を見つけるには x00新しいシンプレックステーブルを作成し、その中で基本変換を実行する必要があります。
a)先頭の行のすべての要素を先頭の要素で除算し、それによって先頭の要素を1に変換します(計算を容易にするため)。
b)先頭の要素(1に等しい)を使用して、先頭の列のすべての要素をゼロに変換します(未知数を削除する方法と同様)。
その結果、新しい基本変数の値がゼロ列で取得されます x 2、x 3、x 4、x 5、(表2を参照)-新しいトップの基本コンポーネント x00(非基本コンポーネント x 1 \ u003d 0、x 6 \ u003d 0、).

表2に示すように、新しい基本ソリューション x00 =(0,10,30,20,40,0)非最適(ゼロ行には非負の推定値7があります)。 したがって、先頭の要素1(表2を参照)を使用して、新しいシンプレックステーブルを作成します。 新しい許容可能な基本的なソリューションを構築します 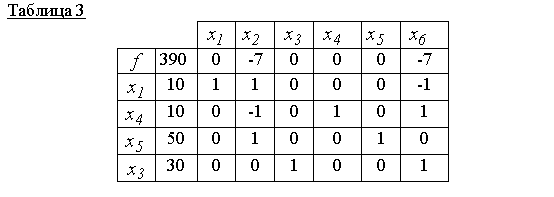
表3は、許容される基本的なソリューションに対応しています。 x000 =(10,0,30,10,50,0)そしてそれは最適です ゼロラインに正のマークはありません。 そう f(x000)= 390目的関数の最小値です。
答え: x000 =(10、0、30、10、50、0)-最小点、 f(x000)= 390.
条件付きで標準的な線形計画問題
リストされている順序で次のタスクを完了する必要があります。- 直接的な問題の最適な計画を見つけます。
a)グラフィカルな方法。
b)シンプレックス法による(初期参照計画の作成には、人工的な基礎法を使用することをお勧めします)。 - 双対問題を作成します。
- 補完的なたるみの条件を使用して、直線のグラフィカルな解から双対問題の最適な計画を見つけます。
- 直接問題を解くことによって得られた最終的なシンプレックスタブローを使用して、最初の双対定理によって双対問題の最適な計画を見つけます(セクション1bを参照)。 「最適解に関する双対問題の目的関数の値は同じです」というステートメントを確認してください。
- シンプレックス法を使用して双対問題を解き、次に、双対問題の最終的なシンプレックステーブルを使用して、最初の双対定理を使用して直接問題の最適な計画を見つけます。 結果をグラフィカルな方法で得られた結果と比較します(段落1aを参照)。
- 最適な整数解を見つけます。
a)グラフィカルな方法。
b)ゴモリー法。
整数ソリューションと非整数ソリューションの関数値を比較します
自制心のための質問
- シンプレックステーブルはどのように構築されますか?
- 基底変換は表にどのように反映されますか?
- シンプレックス法の停止基準を作成します。
- テーブルの再計算を整理する方法は?
- テーブルの再計算を開始するのに便利な行はどれですか。
問題の状態で符号≥の制限がある場合、不等式の両方の部分に-1を掛けることにより、それらを∑a ji bjの形式に減らすことができます。 m個の追加変数xn +j≥0(j = 1、m)を導入し、制約を等式の形式に変換します
![]() (2)
(2)
問題x1、x 2、...、xnのすべての初期変数が非基本であると仮定します。 次に、追加の変数が基本になり、制約システムの特定のソリューションは次の形式になります。
x 1 = x 2 = ... = x n = 0、x n + j = b j、j = 1、m。 (3)
この場合、目標関数F 0 = 0の値なので、F(x)を次のように表すことができます。
F(x)= ∑c i x i + F 0 = 0(4)
初期シンプレックステーブル(シンプレックステーブル1)は、式(2)および(4)に基づいてコンパイルされます。 (2)のように、追加の変数x n + jの前に「+」記号が付いている場合、変数xiおよび自由項bjの前のすべての係数が変更なしでシンプレックステーブルに入力されます。 最大化中の目標関数の係数は、シンプレックステーブルの一番下の行に反対の符号で入力されます。 シンプレックステーブルの無料メンバーが問題の解決策を決定します。
問題を解決するためのアルゴリズムは次のとおりです。
最初のステップ。 フリーメンバー列の要素が検索されます。 それらがすべて正の場合、許容可能な基本的な解決策が見つかりました。最適な解決策を見つけることに対応するアルゴリズムのステップ5に進む必要があります。 最初のシンプレックスタブローに負の自由項がある場合、ソリューションは無効であるため、手順2に進む必要があります。
2番目のステップ。 実行可能な解決策を見つけるために、が実行されますが、基本に含める非基本変数と、基本から削除する変数を決定する必要があります。
表1。
| 基本変数 | 制限のある無料会員 | 非基本変数 | |||||
| x 1 | x2 | ... | x l | ... | x n|||
| xn + 1 | b 1 | 11 | 12 | ... | 1リットル | ... | 1n |
| xn + 2 | b 2 | 21 | 22 | ... | 2リットル | ... | 2n |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| xn + r | b2 | r1 | r2 | ... | rl | ... | rn |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| xn + m | b m | m1 | m2 | ... | aml | ... | amn |
| F(x)max | F0 | -c 1 | -c 2 | ... | -c 1 | ... | -c n |
これを行うには、自由メンバーの列の負の要素のいずれかを選択します(b 2を先頭にするか、許可します。負の自由メンバーのある行に負の要素がない場合、制限のシステムは一貫性がなく、問題には解決策がありません。
同時に、選択したNP x lの増加に伴って最初に符号が変わる変数は、BPから除外されます。 これはxn + rになり、そのインデックスrは条件から決定されます

それらの。 選択した先頭の列の要素に対する自由項の最小の比率に対応する変数。 この関係はと呼ばれます シンプレックス関係。 正のシンプレックス関係のみを考慮する必要があります。
変数xn + rに対応する文字列が呼び出されます リードする、または許可する。 シンプレックステーブルの要素arlは、先頭の行と先頭の列の交点にあり、先頭または解決要素と呼ばれます。主要な要素を見つけると、次のシンプレックスタブローごとに作業が終了します。
3番目のステップ。 新しいシンプレックステーブルが計算され、その要素は前のステップのシンプレックステーブルの要素から再計算され、プライムでマークされます。 b "j、a" ji、c "i、F" 0。 要素は、次の式に従って再計算されます。

最初に、前のシンプレックステーブルで先頭にあった行と列が新しいシンプレックステーブルに入力されます。 式(5)は、先頭の要素の代わりにある要素a "rlが、前のシンプレックステーブルの要素の逆数に等しいことを意味します。行a riの要素は、先頭の要素で除算され、列ajlも先頭の要素で除算されますが、反対の符号が付けられます。要素b "rとc" lは、同じ原理に従って計算されます。
残りの式は、を使用して簡単に記述できます。
長方形は、その対角線の1つが再計算された(ji)要素と先行する(rl)要素によって形成されるように、古いシンプレックステーブルに従って作成されます(図1)。 2番目の対角線は一意に決定されます。 新しい要素a "jiを見つけるには、反対の対角線の要素の積を先頭の要素で割ったものを要素a jiから減算します(これはセルの記号"-"で示されます。同様に要素b" j、(j≠r)およびc "iが再計算されます(i≠l)。
4番目のステップ。 新しいシンプレックステーブルの分析は、アルゴリズムの最初のステップから始まります。 アクションは、実行可能な基本的な解決策が見つかるまで続きます。 フリーメンバー列のすべての要素は正である必要があります。
5番目のステップ。 許容できる基本的な解決策が見つかったと信じています。 ゴール関数F(x)の直線の係数を調べます。 シンプレックステーブルの最適性の兆候は、F行の非基本変数の係数の非負性です。

米。 1.長方形のルール
F行の係数の中に負の係数がある場合(自由項を除く)、別の基本的な解決策に進む必要があります。 目標関数を最大化する場合、基底には非基本変数(たとえば、x l)の基底が含まれ、その列はシンプレックス表の一番下の行の負の係数clの最大絶対値に対応します。 これにより、増加が目標関数の改善につながる変数を選択できます。 変数xlに対応する列は、先頭列と呼ばれます。 同時に、その変数x n + rは基底から除外され、そのインデックスrは最小シンプレックス比によって決定されます。
x n + rに対応する行は先行行と呼ばれ、先行行と先行列の交点にあるシンプレックステーブルの要素arlはと呼ばれます。 主要な要素。
6番目のステップ。 3番目のステップで設定されたルールに従います。 この手順は、最適なソリューションが見つかるか、それが存在しないと結論付けられるまで続きます。
先頭の列の解を最適化する過程で、すべての要素が正でない場合、先頭の行を選択できません。 この場合、問題の許容可能な解の定義域内の関数は上から制限されず、F max->&∞です。
極値の検索の次のステップで、基本変数の1つがゼロに等しくなると、対応する基本解は縮退と呼ばれます。 この場合、いわゆるループが発生します。これは、BPの同じ組み合わせが特定の周波数で繰り返され始め(この場合、関数Fの値が保持されます)、に切り替えることができないという事実によって特徴付けられます。新しい許容可能な基本的なソリューション。 ループはシンプレックス法の主な欠点の1つですが、比較的まれです。 実際には、そのような場合、通常、その列が目標関数の負の係数の最大絶対値に対応する変数を基底に入力することを拒否し、新しい基本解のランダムな選択が行われます。
例1.問題を解決する
max(F(x)= -2x 1 + 5x 2 | 2x 1 +x2≤7; x 1 +4x2≥8;x2≤4;x1.2≥0)
シンプレックス法とソリューションプロセスの幾何学的解釈を与えます。
問題の解決策の図解を図1に示します。 2.ゴール関数の最大値は、座標がODZPの上部で到達します。 シンプレックステーブルを使用して問題を解決しましょう。 2番目の制約に(-1)を掛け、追加の変数を導入して不等式を等式の形式にします。

初期変数x1とx2は非基本と見なされ、追加のx 3、x 4、x 5は基本と見なされ、シンプレックステーブル(シンプレックステーブル2)をコンパイルします。 シンプレックステーブルに対応するソリューション。 2、無効です。 主要な要素は、上記のアルゴリズムのステップ2に従って輪郭が描かれ、選択されます。 次のシンプレックスタブ。 3は、許容される基本的な解決策を定義します。 2主要な要素の概要が示され、問題を解決するためのアルゴリズムの5番目のステップに従って選択されます。 タブ。 4は、問題の最適解に対応します。したがって、次のようになります。x1 = x 5 = 0; x 2 \ u003d 4; x 3 \ u003d 3; x 4 = 8; F max = 20。


米。 2.問題のグラフィカルな解決策
簡単な理論
問題の解決策
モデル構築
それぞれ、第1種、第2種、第3種の商品の売上高を示します。
次に、受け取った利益を表す目的関数:
物的および金銭的資源の制限:
また、タスクの意味に応じて
次の線形計画問題が発生します。
0回目の反復のシンプレックステーブルに入力します。
| BP | シンプレックス 関係 |
8 | 6 | 4 | 0 | 0 | 0 | 0 | 520 | 16 | 18 | 9 | 1 | 0 | 0 | 65/2 | 0 | 140 | 7 | 7 | 2 | 0 | 1 | 0 | 20 | 0 | 810 | 9 | 2 | 1 | 0 | 0 | 1 | 90 | 0 | -8 | -6 | -4 | 0 | 0 | 0 |
最大の問題を解いているので、最大の問題を解くときにインデックスラインに負の数が存在することは、最適な解を受け取っていないこと、および0回目の反復のテーブルからに移動する必要があることを示します。次のもの。
次の反復への移行は次のように実行されます。
先頭の列はに一致します。
キー行は、フリーメンバーと先頭列のメンバーの最小比率(シンプレックス比率)によって決定されます。
キー列とキー行の交点に、有効化要素、つまり7があります。
ここで、最初の反復のコンパイルを開始します。 単位ベクトルの代わりに、ベクトルを導入します。
新しいテーブルでは、allowing要素の代わりに1を書き込み、キー列の他のすべての要素はゼロです。 キー文字列要素は、許容要素によって分割されます。 テーブルの他のすべての要素は、長方形のルールに従って計算されます。
最初の反復のテーブルを取得します。
| BP | シンプレックス 関係 |
8 | 6 | 4 | 0 | 0 | 0 | 0 | 200 | 0 | 2 | 31/7 | 1 | -16/7 | 0 | 1400/31 | 8 | 20 | 1 | 1 | 2/7 | 0 | 1/7 | 0 | 70 | 0 | 630 | 0 | -7 | -11/7 | 0 | -9/7 | 1 | - | 160 | 0 | 2 | -12/7 | 0 | 8/7 | 0 |
最初の反復のキー列はに対応します。
キーラインを見つけます。このために、次のように定義します。
キー列とキー行の交点に、有効化要素があります。 31/7。
基底からベクトルを推定し、ベクトルを入力します。
2回目の反復の表を取得します。
| BP | シンプレックス 関係 |
8 | 6 | 4 | 0 | 0 | 0 | 4 | 1400/31 | 0 | 14/31 | 1 | 7/31 | -16/31 | 0 | 8 | 220/31 | 1 | 27/31 | 0 | -2/31 | 9/31 | 0 | 0 | 21730/31 | 0 | -195/31 | 0 | 11/31 | -65/31 | 1 | 7360/31 | 0 | 86/31 | 0 | 12/31 | 8/31 | 0 |
インデックス行では、すべてのメンバーが負ではないため、線形計画問題の次の解が得られます(空きメンバーの列から書き出す)。
したがって、7.1千ルーブルを売る必要があります。 第1種の商品と45.2千ルーブル。 3番目のタイプの商品。 2番目のタイプの商品は販売するのに不採算です。 この場合、利益は最大になり、237.4千ルーブルになります。 最適な計画を実施する場合、3番目のタイプの残りのリソースは701ユニットになります。
現在はサポートが必要ないが、将来必要になる可能性がある場合は、連絡を失わないようにするために、
線形計画問題を解くためのグラフィカルな方法をすでに理解している場合は、次に進みましょう。 シンプレックス法。 最初のものとは異なり、問題の制限(変数の数、符号の違いなど)は実質的になく、問題のタイプ(M法や人工基底法など)に応じて変更されます。
シンプレックス問題を解く場合、計算は通常(コンパクトさと明確さのために)テーブルで実行され(表形式のシンプレックス法)、最適なソリューションを含む最後のテーブルには、双対問題のソリューション、残りのリソース、情報などの重要な追加情報が含まれます。不足しているリソースなどについて。これにより、線形計画問題の経済分析を行うことができます(以下の例3を参照)。
シンプレックス法を使用して問題を解決する例は、あなたの便宜のために無料で投稿されています-研究し、類似したものを探し、解決します。 この種の割り当てについてサポートが必要な場合は、カスタム線形計画法ソリューションにアクセスしてください。
シンプレックス法を使用した問題の解決:オンラインの例
タスク1。同社はAとBの2つのサイズのバスルーム棚を製造しています。販売代理店は、週に最大550個の棚を市場で販売できると見積もっています。 タイプAの各棚には2m2の材料が必要であり、タイプBの棚には3m2の材料が必要です。 同社は週に最大1200m2の資材を受け取ることができます。 タイプAの棚を1つ製造する場合は、12分の機械時間が必要であり、タイプBの棚を1つ製造する場合は、30分かかります。 機械は週に160時間使用できます。 タイプAの棚の販売からの利益が3通貨単位であり、タイプBの棚からの利益が4デンである場合。 ユニット、各タイプの棚を1週間にいくつ生産する必要がありますか?
数学モデルを作成し、シンプレックス法でLLPを解く(pdf、33 Kb)
タスク2。シンプレックス法を使用して線形計画問題を解きます。 
人工的な基礎を用いたシンプレックス法による解法(pdf、45 Kb)
タスク3。同社は2種類の原材料を使用して、A1、A2、A3の3種類の製品を生産しています。 生産単位あたりの各タイプの原材料のコスト、計画期間の原材料の在庫、および各タイプの生産単位あたりの利益がわかっています。
- 利益を最大化するには、各タイプの製品をいくつ生産する必要がありますか?
- 各タイプの原材料のステータスとその特定の値を決定します。
- 各タイプの原材料の在庫を変更するための最大間隔を決定します。その範囲内で、最適な計画の構造、つまり リリースの命名法は変更されません。
- 希少な種類の原材料の1つの在庫が可能な最大値(指定された生産量の命名法の範囲内)に増加したときの生産量と生産からの利益を決定します。
- 結果として得られる最適な計画が変更されない、各タイプの生産単位からの利益の変化の間隔を決定します。
経済分析による線形計画問題の解決(pdf、163 Kb)
タスク4。シンプレックス法を使用して線形計画問題を解きます。 
参照計画の検索を伴う表形式のシンプレックス法による解決策(pdf、44 Kb)
タスク5。シンプレックス法を使用して線形計画問題を解きます。 
表形式のシンプレックス法による解法(pdf、47 Kb)
タスク6。シンプレックス法を使用して問題を解決します。最初の参照計画として、次の条件で与えられた計画を考慮します。 
手動シンプレックス法による解決策(pdf、60 Kb)
タスク7。修正されたシンプレックス法で問題を解決します。
2種類の製品AとBの製造には、3種類の技術設備が使用されます。 製品Aのユニットの生産では、第1タイプの機器はa1 = 4時間、第2タイプの機器はa2 = 8時間、第3タイプの機器はa3 = 9時間使用されます。 製品Bのユニットの生産には、第1タイプの機器b1 = 7時間、第2タイプの機器b2 = 3時間、第3タイプの機器b3 = 5時間が使用されます。
これらの製品の製造では、第1タイプの機器はt1 = 49時間以内、第2タイプの機器はt2 = 51時間以内、第3タイプの機器はt3 = 45時間以内で稼働できます。
完成品Aのユニットの販売による利益は、ALPHA = 6ルーブル、製品B-BETTA = 5ルーブルです。
製品AおよびBの生産計画を作成し、それらの販売から最大の利益を提供します。
修正シンプレックス法による解法(pdf、67 Kb)
タスク8。デュアルシンプレックス法で最適解を見つける 
デュアルシンプレックス法による解法(pdf、43 Kb)
線形計画法の問題に対する解決策の例
線形計画問題を解くための方法
線形計画問題のサポートソリューション
線形計画問題を標準形で与えましょう
条件下で
システム(2)–(3)の解のセットで示します。 ここで、は行列の階数であり、はシステム(2)の方程式の数であると仮定します。
行列の列ベクトルのシステムから、ベクトルの線形独立サブシステムを選択します。 存在するからです。 このシステムは、の基礎を形成します。 、で示します。 電話しましょう 基本値のセット 索引 、 - 基本的な部分行列 行列。 ベクトルの座標を呼び出します 基本 、 もしも 非基本 それ以外は。
システム(2)をとして記述します。 左側の用語を基本的な用語と基本的でない用語に分けてみましょう。
このシステムの特定のソリューションを次のように定義します。 (4)すべての非基本変数をゼロに設定しましょう。 次に、システム(4)は次の形式を取ります
(5)と呼びましょう 基本サブシステム 連立方程式(2)。 ベクトルの基本座標で構成されるベクトルで表します。 次に、システム(2)をベクトル行列形式で書き直すことができます。
部分行列は基本的であるため、
非縮退。 したがって、システム(6)には独自のソリューションがあります。 このようにして得られたシステム(2)の特定の解は次のように呼ばれます。 リファレンスソリューション 基底に対応する直接線形計画問題。 (参照ソリューションは、 基本 )。 ご覧のとおり、基礎は独自の参照ソリューションに対応しています。 明らかに、サポートソリューションの数は有限です。
これに基づいて、二重線形計画問題の参照解も定義します。 標準的な問題と二重の問題は次の形式を持っていることを思い出してください
条件下で
システム(8)を次のように記述します
システム(8)の解のセットは。で示されることを思い出してください。
システム(9)の基本制約が満たされる条件から双対変数のベクトルを等式として定義しましょう。 次の連立一次方程式が得られます。
ba-で構成されるベクトルで表す
ベクトルのsis座標。 次に、システム(10)をベクトル行列形式で書き直すことができます。
システム(11)にも独自のソリューションがあります。
それを呼びましょう 極めて重要 (基本 )決断 基底に対応する二重線形計画問題。 この参照ソリューションも一意に決定されます。
したがって、任意の基底は2つのベクトルに対応します。2つの参照解と線形計画法の直接問題と双対問題です。
次に、以下のタイプのベースとサポートソリューションを定義します。 参照解のすべての座標が負でない場合、この参照解が対応する基準は次のように呼ばれます。 許容可能 リファレンスプラン 直接線形計画問題であり、同じ基底に対応する参照解はと呼ばれます 疑似計画 デュアルタスク。 実際、基底の許容性については、基底座標が非負であることが十分です。 基本計画は、直接線形計画問題()の有効なベクトルであることに注意してください。
参照解が双対問題のすべての制約(9)を満たす場合、この参照解が対応する基礎はと呼ばれます。 二重に認められる 。 この場合、ベクトルは呼び出されます リファレンスプラン 線形計画法の双対問題、および同じ基礎に対応する参照解
と呼ばれる 疑似計画 直接タスク。
基底の二重許容性については、非基底の不等式のみが成り立つことで十分です。 ベースラインは、二重線形計画問題の許容ベクトルであることに注意してください()。
不等式(9)の左と右の部分の違いは、で示されます。 次に、すべての非負性をチェックすることにより、基礎の二重許容性を確立できます。 定義から直接次のように、すべての基本残差はゼロ()に等しいことに注意してください。
シンプレックス法による直接問題と双対問題の解決例
したがって、すべてのに不等式が当てはまることを確認するだけで十分です。
定理1。させてといくつかの基礎に対応する線形計画問題の参照解です、そして平等 .
証拠 . サポートソリューションの定義から、同等性を簡単に取得できます
ここで、定理の妥当性が続きます。
定理2。 (サポートソリューションの最適性基準) 基礎が同時に許容され、二重に許容され、その後、対応するサポートソリューションとそれぞれ、線形計画法の直接問題と双対問題の解決策です。
証拠。 このステートメントの妥当性は、線形計画法の双対性の理論と定理1に基づいています。
定理3。問題(1)-(3)の実行可能な解決策は、それが凸多面体集合の頂点である場合に限り、問題の基本計画です。
証拠。 させて –基本的なタスクプラン(1)–(3)。 それを証明しましょう -セットのトップ . 定義上、ベースライン – いくつかの基礎に対応する許容可能な参照ソリューション、すなわち – 変数に関する連立一次方程式の解
このシステムが独自のソリューションを持っていることは容易に理解できます。 したがって、点を含む面の方位面 , 次元は0です。したがって、 -セットのトップ .
戻る。 させて セットの一番上です。 それを証明しましょう –基本的なタスクプラン(1)–(3)。 頂点であるため、次元がゼロに等しいセットの面です。 したがって、ベクトル 少なくともゼロのコンポーネントがあり、その数のセットを示します . この上、 – システムの唯一の解決策
どこ . したがって、ベクトルのシステムが線形独立であることを証明することは残っています。 反対のことを想定しましょう。 次に、すべてがゼロに等しくない数があります。たとえば、。 そう
これは、システム(12)がとは異なるソリューションを持っていることを意味します 、これはそのソリューションの独自性と矛盾します。 したがって、は基底であり、ベクトル 問題の対応する基本計画です(1)-(3)。 それが必要だったのです。
問題(7)、(8)(双対問題(1)-(3))の許容可能な解決策も、許容集合の頂点である場合に限り、サポートプランであることに注意してください。
発行日:2015-01-10; 読む:695 | ページの著作権侵害
Studopedia.org-Studopedia.Org-2014-2018。(0.005秒)..。
明確にするために、最小値を見つける問題が解決されていると仮定します。
1.線形計画問題を標準形に減らします。
追加の変数を導入した後、連立方程式と線形関数は拡張システムと呼ばれる形式で記述されます。
すべての追加の変数は、無料のメンバーと同じ符号を持っていると想定しています。 それ以外の場合は、いわゆる M以下で説明する方法です。
2.基本変数と自由変数を定義します。
3.元の拡張システムを最初のシンプレックステーブルに入力します。 線形目的関数の方程式を含む表の最後の行は、次のように呼ばれます。 鑑定。 ゴール関数の係数を指定します。 表の左側の列に、主な変数(基本)を書き留め、後続の変数(自由変数の係数)を書き留めます。 最後から2番目の列-拡張システムの無料メンバー。 最後の列は、関係(6.29)に基づいて基本変数を決定するために必要な推定比率のために用意されています。
4.定理6.7、…、6.9に従って値によって問題を解決する可能性を判断します。
5.解決(参照)要素を選択します。
表形式のシンプレックス法による生産問題の解決
最適性の基準が満たされない場合(定理6.7または6.8の条件が満たされない場合)、最後の行の絶対値が最大の負の係数が解決(参照)列を決定します。 ![]() .
.
次のルールに従って、各行の推定比率を作成します。
1 0)すべてで、異なる符号がある場合。
2 0)すべての場合と;
3 0)if;
4 0)0ifおよび;
5 0)とが同じ符号を持っている場合。
を定義しましょう。 有限の最小値がない場合、問題には有限の最適値()がありません。 最小値が有限の場合は、行を選択します qに到達し(複数ある場合は任意)、これを解決(参照)文字列と呼びます。 解決する行と列の交点に、解決(参照)要素があります。
6 0)ルールに従って次のテーブルに移動します。
a)左側の列に、新しい基準を記述します。メイン変数の代わりに、変数、つまり 変数を交換し、;
b)参照要素の代わりに1を配置します。
c)元のテーブルの要素を新しいテーブルの残りの参照行に残します。
d)元のテーブルの対応する要素に-1を掛けて、参照列の残りの場所に配置します。
e)新しいテーブルの要素、、の残りの空き領域に、次のように番号、、、を書き込みます。
これらの式を使用して計算を簡略化するために、次のように式化できます。 「長方形のルール」(図6.8):頂点を持つ長方形の対角線上の要素(または、、、、、または、、、)が乗算され(参照要素を含まない積はマイナス記号で取得されます)、結果の積は次のようになります。追加した;
f)新しいテーブルのすべての受信要素を参照要素に分割します。
7 0)要素の値に基づいて、目的関数の最適値が見つかったかどうかを判断します。 答えが否定的な場合は、決定を続けます(ポイント6に戻ります)。
米。 6.8。 数値を定義するための長方形の規則:
a −、b −、c −。
縮退していない許容可能な基本解のためにシンプレックステーブルを変換するためのアルゴリズム。 定理6.9で記述された状況は満たされました。 元の線形計画問題が縮退している場合、シンプレックス法による解の過程で、縮退した基本解も現れる可能性があります。 この場合、シンプレックス法のアイドルステップが可能です。 ここでの反復 f(バツ)変わりません。 ループすることも可能です。 アイドルステップの無限のシーケンス。 それを防ぐために、特別なアルゴリズムが開発されました-アンチサイクリン。 ただし、圧倒的多数の場合、アイドル状態のステップは目的関数が減少するステップに置き換えられ、解法プロセスは有限回の反復後に終了します。
例6.8。シンプレックス法を使用して、例6.7に示されている問題を解決します。
⇐前へ45678910111213次へ⇒
発行日:2015-01-23; 読む:174 | ページの著作権侵害
Studopedia.org-Studopedia.Org-2014-2018。(0.002秒)..。
ホーム>>例3。 シンプレックス法。 関数の最大値を見つける(人工ベース)
シンプレックス法
| — | x 1 | + | x2 | ≥ | 1 | |
| x 1 | + | 3 | x2 | ≤ | 15 | |
| — | 2 | x 1 | + | x2 | ≤ | 4 |
| 変数が係数1で与えられた方程式に入り、残りの方程式に含まれていない場合、変数は与えられた方程式の基本と呼ばれます(方程式の右側に正の数がある場合)。 すべての方程式に基底変数がある場合、システムには基底があると言われます。 シンプレックス法の考え方は、ある基底から別の基底に移動して、少なくとも既存の基底よりも小さい関数値を取得することです(各基底は単一の関数値に対応します)。 ある基盤から別の基盤への移行はどのように実行されますか? |
| x 1 = 0 x 2 = 0 S 1 = 0 S 2 = 15 S 3 = 4 R 1 = 1 |
=> W = 1 |
| x 1 | x2 | S1 | S2 | S3 | R1 | 聖。 メンバー | Θ |
| -1 | 1 | -1 | 0 | 0 | 1 | 1 | 1: 1 = 1 |
| 1 | 3 | 0 | 1 | 0 | 0 | 15 | 15: 3 = 5 |
| -2 | 1 | 0 | 0 | 1 | 0 | 4 | 4: 1 = 4 |
| 1 | -1 | 1 | 0 | 0 | 0 | W-1 | |
| -1 | 1 | -1 | 0 | 0 | 1 | 1 | |
| 4 | 0 | 3 | 1 | 0 | -3 | 12 | |
| -1 | 0 | 1 | 0 | 1 | -1 | 3 | |
| 0 | 0 | 0 | 0 | 0 | 1 | W-0 |
| x 1 | x2 | S1 | S2 | S3 | 聖。 メンバー | Θ |
| -1 | 1 | -1 | 0 | 0 | 1 | |
| 4 | 0 | 3 | 1 | 0 | 12 | 12: 4 = 3 |
| -1 | 0 | 1 | 0 | 1 | 3 | |
| 4 | 0 | 1 | 0 | 0 | F-1 | |
| -1 | 1 | -1 | 0 | 0 | 1 | |
| 1 | 0 | 3/4 | 1/4 | 0 | 3 | |
| -1 | 0 | 1 | 0 | 1 | 3 | |
| 4 | 0 | 1 | 0 | 0 | F-1 | |
| 0 | 1 | -1/4 | 1/4 | 0 | 4 | |
| 1 | 0 | 3/4 | 1/4 | 0 | 3 | |
| 0 | 0 | 7/4 | 1/4 | 1 | 6 | |
| 0 | 0 | -2 | -1 | 0 | F-13 |
| S1 = 0 S2 = 0 x 1 = 3 x 2 = 4 S 3 = 6 |
=> F-13 = 0 => F = 13 |
選択した行係数の中に正の係数はありません。 したがって、関数Fの最大値が見つかります。
答え:
x 1 = 3 x 2 = 4
F max = 13
あなたの問題の解決に行きなさい
©2010-2018、すべての質問については、 [メール保護]
タスク
3つのグループの商品を実装するために、営利企業には、b 1 = 240、b 2 = 200、b 3 = 160単位の3種類の限られた材料および金銭的リソースがあります。 同時に、1グループの商品を1,000ルーブルで販売します。 売上高では、最初のタイプのリソースは11 = 2ユニットの量で消費され、2番目のタイプのリソースは21 = 4ユニットの量で消費され、3番目のタイプのリソースは31 = 4の量で消費されます。単位。 1000ルーブルの商品の2つおよび3つのグループの販売のため。 売上高は、それぞれ、12 = 3、13 = 6ユニットの量の最初のタイプのリソース、22 = 2、23 = 4ユニットの量の2番目のタイプのリソース、リソースに費やされます。 32 = 6、33 = 8ユニットの量の3番目のタイプの。 1000ルーブルあたり3グループの商品の販売からの利益
LLPを解くためのシンプレックス法
こする。 売上高は、それぞれc 1 \ u003d 4、c 2 \ u003d 5、c 3 \ u003d 4(千ルーブル)です。 貿易企業の利益が最大化されるように、貿易売上高の計画された量と構造を決定します。
商品流通計画の直接的な問題に対して、 可解シンプレックス法、作曲 双対問題線形計画。
インストール 変数の共役ペア直接問題と双対問題。
変数の共役ペアに従って、直接問題の解から、次のようになります。 双対問題の解決策、 その中で リソースの見積もり商品の販売に費やした。
メソッドによるシンプレックス問題の解決
x 1、x 2、x 3-販売された商品の数(千ルーブル)、それぞれ1、2、3-彼女のグループとします。 次に、問題の数学的モデルは次の形式になります。
F = 4 x 1 + 5 x 2 + 4 x 3-> max

この方法でシンプレックスを解きます。
不等式を等式に変換するために、追加の変数x4≥0、x5≥0、x6≥0を導入します。

基礎として、x 4 \ u003d240を取ります。 x5 = 200; x6 = 160。
データはに入力されます シンプレックステーブル
シンプレックステーブル番号1

対象機能:
 0240 + 0200 + 0160 = 0
0240 + 0200 + 0160 = 0
次の式に従ってスコアを計算します。

Δ1\ u003d 0 2 + 0 4 + 0 4-4 \ u003d-4
Δ2\ u003d 0 3 + 0 2 + 0 6-5 \ u003d-5
Δ3\ u003d 0 6 + 0 4 + 0 8-4 \ u003d-4
Δ4\ u003d 0 1 + 0 0 + 0 0-0 \ u003d 0
Δ5\ u003d 0 0 + 0 1 + 0 0-0 \ u003d 0
Δ6\ u003d 0 0 + 0 0 + 0 1-0 \ u003d 0
負の見積もりがあるため、計画は最適ではありません。 最低評価:
変数x2を基底に導入します。
基底を離れる変数を定義します。 これを行うために、列x2の最小の非負の比率を見つけます。
![]()
![]()
![]() = 26.667
= 26.667
最小の非負:Q 3 = 26.667。 基礎から変数x6を導き出します
3行目を6で割ります。
1行目から3行目を減算して3を掛けます
2行目から3行目を減算して2を掛けます

計算します:
![]()
![]()
![]()
![]()
![]()
新しいテーブルを取得します。
シンプレックステーブル番号2

対象機能:
 0160 + 0 440/3 + 5 80/3 = 400/3
0160 + 0 440/3 + 5 80/3 = 400/3
次の式に従ってスコアを計算します。

Δ1\ u003d 0 0 + 0 8/3 + 5 2 / 3-4 \ u003d-2 / 3
Δ2\ u003d 0 0 + 0 0 + 5 1-5 \ u003d 0
Δ3\ u003d 0 2 + 0 4/3 + 5 4 / 3-4 \ u003d 8/3
Δ4\ u003d 0 1 + 0 0 + 5 0-0 \ u003d 0
Δ5\ u003d 0 0 + 0 1 + 5 0-0 \ u003d 0
Δ6\ u003d 0(-1)/ 2 + 0(-1)/ 3 + 5 1 / 6-0 \ u003d 5/6
負の推定値Δ1= -2 / 3があるため、計画は最適ではありません。
変数x1を基底に導入します。
基底を離れる変数を定義します。 これを行うために、列x1の最小の非負の比率を見つけます。
![]()


最小の非負:Q 3 \ u003d40。変数x2を基底から導出します
3行目を2/3で割ります。
2行目から3行目を減算して8/3を掛けます

計算します:
![]()
![]()
![]()
新しいテーブルを取得します。
シンプレックステーブル番号3

対象機能:
 0160 + 0 40 + 4 40 = 160
0160 + 0 40 + 4 40 = 160
次の式に従ってスコアを計算します。

Δ1\ u003d 0 0 + 0 0 + 4 1-4 \ u003d 0
Δ2\ u003d 0 0 + 0(-4)+ 4 3 / 2-5 \ u003d 1
Δ3\ u003d 0 2 + 0(-4)+ 4 2-4 \ u003d 4
Δ4\ u003d 0 1 + 0 0 + 4 0-0 \ u003d 0
Δ5\ u003d 0 0 + 0 1 + 4 0-0 \ u003d 0
Δ6\ u003d 0(-1)/ 2 + 0(-1)+ 4 1 / 4-0 \ u003d 1
マイナスの見積もりがないので、計画が最適です。
問題の解決策:
答え
x 1 = 40; x2 = 0; x 3 \ u003d 0; x 4 = 160; x5 = 40; x6 = 0; F max = 160
つまり、最初のタイプの商品を4万ルーブルで販売する必要があります。
こする。 2番目と3番目のタイプの商品を販売する必要はありません。 この場合、最大利益はF max = 160千ルーブルになります。
双対問題の解決
双対問題は次のようになります。
Z = 240 y 1 + 200 y 2 + 160 y 3-> min

不等式を等式に変換するために、追加の変数y4≥0、y5≥0、y6≥0を導入します。

直接問題と双対問題の変数の共役ペアは、次の形式になります。
直接問題の最後のシンプレックス表3から、双対問題の解決策が見つかります。
Z min = F max = 160;
y 1 \u003dΔ4\ u003d 0; y 2 \u003dΔ5\ u003d 0; y 3 \u003dΔ6\ u003d 1; y 4 \u003dΔ1\ u003d 0; y 5 \u003dΔ2\ u003d 1; y 6 \u003dΔ3\ u003d 4;
答え
y1 = 0; y2 = 0; y 3 = 1; Z min = 160;
シンプレックス法は、ある基本点(基本解)から別の基本点(基本解)に移動するときの解の連続的な改善の原理に基づく計算手順です。 同時に、目的関数の値が向上します。
基本的な解決策は、許容値の領域の頂点にある許容可能な解決策の1つです。 シンプレックスの頂点ごとに最適性をチェックすると、目的の最適値に到達します。 シンプレックス法はこの原理に基づいています。
シンプレックスは、同じ超平面に存在しないn + 1個の頂点を持つn次元空間の凸多角形です(超平面は空間を2つの半空間に分割します)。
たとえば、予算制約のラインは、商品を利用可能と利用不可に分割します。
最適解が存在する場合、「ループ」の場合を除いて、有限回数の反復(ステップ)の後にそれが見つかることが証明されています。
シンプレックス法のアルゴリズムは、いくつかの段階で構成されています。
第一段階。 初期最適化モデルが構築されます。 さらに、条件の初期行列は、縮小された標準形に変換されます。これは、他のすべての標準形の中で際立っています。
a)条件の正しい部分(自由項bi)は非負の値です。
b)条件自体が平等である。
c)条件の行列には、完全な同一性の部分行列が含まれます。
自由項が負の場合、不等式の両側に-1が掛けられ、不等式の符号が逆になります。 不等式を等式に変換するために、追加の変数が導入されます。これは通常、十分に活用されていないリソースの量を示します。 これが彼らの経済的意味です。
最後に、追加の変数を追加した後、条件行列に完全な恒等式部分行列が含まれていない場合、経済的に意味のない人工変数が導入されます。 これらは、アイデンティティサブマトリックスを取得し、シンプレックス法を使用して問題を解決するプロセスを開始するためにのみ導入されています。
問題の最適な解決策では、すべての人工変数(IP)がゼロに等しくなければなりません。 これを行うために、最大の問題を解決するときに大きな負の係数(-M)を使用し、最小の問題を解決するときに大きな正の係数(+ M)を使用して、問題の目的関数に人工変数を導入します。 この場合、人工変数のゼロ以外の小さな値でも、目的関数の値が急激に減少(増加)します。 通常、Mは主変数の係数の値の1000倍である必要があります。
第二段階。 初期のシンプレックステーブルが作成され、いくつかの初期の基本的な解決策が見つかります。 IDサブマトリックスを形成する変数のセットは、最初の基本的なソリューションとして採用されます。 これらの変数の値は、無料のメンバーと同じです。 他のすべての非基本変数はゼロに等しくなります。
サードステージ。 基本解の最適性のチェックは、目的関数の係数の特別な推定値を使用して実行されます。 目的関数の係数のすべての推定値が負またはゼロに等しい場合、既存の基本解が最適です。 目的関数係数の少なくとも1つの推定値がゼロより大きい場合、既存の基本解は最適ではなく、改善する必要があります。
第4段階。 新しい基本ソリューションに移行します。 このような変数を最適な計画に導入する必要があることは明らかです。これにより、目的関数が最大限に向上します。 利益を最大化するための問題を解決するとき、最適な計画は、生産が最も収益性の高い製品を導入します。 これは、目的関数係数推定の最大の正の値によって決定されます。
指定された反復でこの番号を持つシンプレックステーブルの列は、一般列と呼ばれます。
一般行を見つけるために、すべての空きメンバー(リソース)が一般列の対応する要素に分割されます(製品の単位あたりのリソース消費率)。 得られた結果から、最小のものが選択されます。 特定の反復でそれに対応する線は、一般線と呼ばれます。 これは、特定の反復での生産を制限するリソースに対応します。
一般的な列と行の交点にあるシンプレックステーブルの要素は、一般的な要素と呼ばれます。
次に、一般文字列のすべての要素(フリーメンバーを含む)が一般要素で除算されます。 この操作の結果、一般要素は1に等しくなります。 さらに、一般的な列の他のすべての要素がゼロに等しくなる必要があります。 一般的な列は単一になるはずです。 すべての文字列(一般文字列を除く)は次のように変換されます。 新しい行の結果の要素は、一般列の対応する要素で乗算され、結果の積は、古い行の要素から減算されます。
新しい基本変数の値は、空きメンバー列の対応するセルで取得されます。
第5段階。 得られた基本解は、最適性がチェックされます(第3段階を参照)。 最適な場合、計算は停止します。 それ以外の場合は、新しい基本的な解決策(第4段階)などを見つける必要があります。
シンプレックス法
シンプレックス法による線形計画法の最適化問題の解法の例
2種類の製品(x1とx2)の生産に最適な計画を見つける必要があります。
初期データ:
最適化モデルを構築しましょう
–リソースAの制限。
-リソース制限B。
問題を縮小された標準形に縮小しましょう。 これを行うには、追加の変数X3およびX4を導入するだけで十分です。 その結果、不等式は厳密な等式に変換されます。
最初のシンプレックスタブローを作成し、最初の基本的なソリューションを見つけます。 これらはアイデンティティサブマトリックスに対応するため、追加の変数になります。
最初の反復。 一般的な列と一般的な行を見つけます。
![]()
一般的な要素は5です。
2回目の反復。 見つかった基本的なソリューションは最適ではありません。 推定値の文字列(Fj-Cj)には、1つの正の要素が含まれています。 一般的な列と一般的な行を見つけます。
max(0,0.3、-1.4,0)= 0.2
![]()
目的関数Fj– Cjのすべての特別な推定値はゼロまたは負であるため、見つかった解は最適です。 F(x)= 29x1 = 2; x2 = 5。
これは、シンプレックス法(アプレットではない)による2つの問題の手動(アプレットではない)ソリューションであり、シンプレックス法で問題を解決するためのアルゴリズムを理解するための詳細な説明が含まれています。 最初の問題には「≤」(初期基底の問題)のみの不等式記号が含まれ、2番目の問題には「≥」、「≤」または「=」(人工基底の問題)の記号を含めることができます。これらは異なる方法で解決されます。方法。
シンプレックス法、初期ベースの問題の解決
1)シンプレックス法初期ベースの問題の場合(制約の不等式のすべての兆候は「≤」です)。
問題を書いてみましょう カノニカルフォーム、つまり 不等式制約を等式として書き直し、追加します バランスシート変数:

このシステムは基底を持つシステムであり(基底s 1、s 2、s 3、それぞれが係数1のシステムの1つの方程式にのみ含まれます)、x1とx2は自由変数です。 シンプレックス法を使用する問題には、次の2つの特性が必要です。-制約のシステムは、基底を持つ連立方程式である必要があります。 -システム内のすべての方程式の自由項は負でない必要があります。
結果として得られるシステムは、基礎を持つシステムであり、その自由項は負ではないため、適用できます。 シンプレックス法。 問題を解決するための最初のシンプレックステーブル(反復0)をコンパイルします。 シンプレックス法、つまり 目的関数の係数の表と対応する変数の連立方程式。 ここで、「BP」は基本変数の列を意味し、「ソリューション」はシステムの方程式の正しい部分の列を意味します。 解決策は最適ではありません。 z線には負の係数があります。
シンプレックス法の反復0
|
態度 |
|||||||
ソリューションを改善するために、次の反復に進みましょう シンプレックス法、次のシンプレックスタブローを取得します。 このためにあなたは選ぶ必要があります 列を有効にする、つまり シンプレックス法の次の反復で基底に入る変数。 これは、z行の最大の負の係数(最大の問題)によって選択されます。シンプレックス法の最初の反復では、これは列x 2(係数-6)です。
次に、 許可文字列、つまり シンプレックス法の次の反復で基底を残す変数。 これは、「決定」列と解決列の対応する正の要素(「比率」列)の最小の比率によって選択されます。最初の反復では、これは行s 3(係数20)です。
許容要素は、解決列と解決行の交点にあり、そのセルは色で強調表示され、1に等しくなります。したがって、シンプレックス法の次の反復で、変数x2が基本のs1に置き換わります。 リレーションはz文字列で検索されないことに注意してください。ダッシュ「-」がそこに配置されます。 最小比率が同じである場合は、それらのいずれかが選択されます。 解像度列のすべての係数が0以下の場合、問題の解は無限大です。
次の表「反復1」に記入してみましょう。 「反復0」テーブルから取得します。 さらに変換する目的は、x2有効化列を単一の列に変換することです(有効化要素の代わりに1つ、残りの要素の代わりにゼロを使用)。
1)「反復1」テーブルの行x2を計算します。 まず、「反復0」テーブルの解決行s 3のすべてのメンバーを、このテーブルの解決要素(この場合は1に等しい)で除算し、「反復1」テーブルの行x2を取得します。 。 なぜなら この場合の解決要素は1に等しいので、「反復0」テーブルの行s3は「反復1」テーブルの行x2と一致します。 0 1 0 0 120を取得した「反復1」テーブルの行x2、「反復1」テーブルの残りの行は、この行と「反復0」テーブルの行から次のように取得されます。
2)「反復1」テーブルのz行の計算。 「反復0」テーブルの列x2の最初の行(z行)の-6の代わりに、「反復1」テーブルの最初の行に0が必要です。 これを行うには、「反復1」テーブルの行x 2のすべての要素に6を掛け、0 6 0 0 6 120を取得し、この行に最初の行を追加します(z-行) 「反復0」テーブルの-4-6 0 0 0 0の場合、-4 0 0 0 6120が得られます。x2列にゼロ0が表示され、目標が達成されました。 権限列x2の要素は赤で強調表示されます。
3)「反復1」テーブルの行s1の計算。 「反復1」テーブルの「反復0」テーブルの1行の1の代わりに、「反復1」テーブルの0にする必要があります。 これを行うには、「反復1」テーブルの行x 2のすべての要素に-1を掛け、0 -1 0 0 -1 -20を取得し、この行にs1-を追加します。 「反復0」テーブルの行21 1 0 0 64、行2 0 1 0 -144を取得します。必要な0はx2列で取得されます。
4)「反復1」テーブルの行s2の計算。 「反復0」テーブルの2行の3の代わりに、「反復1」テーブルの0にする必要があります。 これを行うには、「反復1」テーブルの行x 2のすべての要素に-3を掛け、0 -3 0 0 -3 -60を取得し、この行にs1-を追加します。 「反復0」テーブルの行13 0 1 0 72、行1 0 0 1 -3 12.を取得します。必要な0は、x2列で取得されます。「反復1」テーブルのx2列には、シングルになると、1つが1になり、残りは0になります。
「反復1」テーブルの行は、次のルールに従って取得されます。
新しい行=古い行-(古い行のアクセス許可係数)*(新しい行)。
たとえば、z-lineの場合、次のようになります。
古いz文字列(-4 -6 0 0 0 0)-(-6)*新しい有効化文字列-(0 -6 0 0 -6 -120)=新しいz文字列(-4 0 0 0 6120)。
以下のテーブルでは、テーブル要素の再計算も同様の方法で行われるため、省略します。
シンプレックス法の反復1
|
態度 |
|||||||
許容列x1、許容行s 2、s 2は基底を離れ、x1は基底に入ります。 まったく同じ方法で、z行にすべての正の係数を持つテーブルが取得されるまで、残りのシンプレックステーブルを取得します。 これは、最適なテーブルの兆候です。
シンプレックス法の反復2
|
態度 |
|||||||
列s3を解決し、行s 1を解決すると、s 1が基底を離れ、s3が基底に入ります。
シンプレックス法の反復3
|
態度 |
|||||||
z行では、すべての係数が非負であるため、最適解x 1 = 24、x 2 = 16、z max = 192が得られます。



















