ピークの公式による面積の求め方 ピークの式を使用して数字の面積を求める
ピックの式
はじめに
フォーミュラピーク。 私の証明
証明II。
Shの証明
3.タスク
4.頂点の座標を通る多角形の面積の公式。
5.タスク
6.文学
ピックの式
はじめに
物語の中で私たちは知恵を描きます、
詩で - ウィット、
数学で - 洞察力。
F.ベーコン
プロットは通常の市松模様の紙の上に展開されます。
セルの側面に沿って伸びる線がグリッドを形成し、セルの上部がこのグリッドのノードを形成します。 シート上の節点に頂点を持つ多角形を描き、その面積を見つけます。
あなたはさまざまな方法でそれを検索することができます。 たとえば、多角形をかなり単純な形にカットし、その面積を見つけてそれらを折り畳むことができます。
しかし、ここで我々は多くのトラブルを待っています。 図形は長方形、台形、および三角形に簡単に分割され、その面積は簡単に計算されます。
多角形は非常に単純に見えますが、その面積を計算するために一生懸命努力する必要があります。 多角形がもっと奇妙に見えたら? 頂点がグリッドの節点に位置する多角形の面積ははるかに簡単に計算できます。それらの面積と、多角形の内側および境界上にある節点の数を結ぶ式があります。 この素晴らしく単純な方式はピーク方式と呼ばれます。
フォーミュラピーク。
多角形の頂点(必ずしも凸状ではない)は、整数格子の節点にあります。 その中には、格子のB節点があり、G節点の境界にあります。 その面積がB +と等しいことを証明しましょう  - 1(ピック式)
- 1(ピック式)
私の証明
頂点が整数格子の節点にある、つまり、それらが整数座標を持つ多角形を考えてみましょう。

多角形を、節点が内側にも側面にも含まれていない格子ノード内の頂点を持つ三角形に分割します。

を意味します。
n - 多角形の辺の数
メートル - 格子節点に頂点があり、内側にも側面にも結び目を含まない三角形の数
B - 多角形内のノード数
G - 頂点を含む、辺上のノード数
これらすべての三角形の面積は同じで等しい。
したがって、多角形の面積は  .
.
180 0 メートル .
今、私たちは別の方法でこの量を見つけるでしょう。
任意の内部ノードの頂点との角度の合計は360°です。
その場合、すべての内部ノードの頂点と角の合計は360 0 Vです。
辺ではなく頂点での節点での角度の合計は180 0(G - n).
多角形の頂点の角度の合計は180 0( n – 2) .
すべての三角形の角度の合計は 360 0 V + 180 0(D - n) + 180 0 (n – 2).
だから180 0 メートル = 360 0 V + 180 0(G - n) + 180 0 (n – 2),
180 0 メートル = 360 0 V + 180 0 D - 180 0 n + 180 0 n - 180 0・2、
180 0 メートル = 360 0 V + 180 0 D – 360 0、
 = B +
= B +  – 1 ,
– 1 ,
多角形の面積Sの式を取得します。
S= B +  – 1 ,
– 1 ,
ピークの式として知られています。
図では、B = 24、G = 9、S = 24 + – 1 = 27,5.

Peak式を使って最初の多角形の面積を求めます。

B = 28(緑色の点)。
G = 20(青い点)
S =を取得  = 37平方ユニット
= 37平方ユニット
証明II。
整数格子の節点に頂点をもつ各多角形Mに、数f(M)を割り当てる。  ここで、総和はMに属するすべてのグリッドノードにまたがり、角度は
ここで、総和はMに属するすべてのグリッドノードにまたがり、角度は  次のように定義されています。
次のように定義されています。 ![]() =
=  多角形の内側の点
多角形の内側の点  =
=  頂点以外の境界点の場合
頂点以外の境界点の場合  - このノードが頂点の場合は、頂点の角度 f(M)=であることは簡単にわかります
- このノードが頂点の場合は、頂点の角度 f(M)=であることは簡単にわかります  +
+  = B +
= B +  1.数f(M)が多角形Mの面積に等しいことを検証するために残る。
1.数f(M)が多角形Mの面積に等しいことを検証するために残る。
多角形Mを格子の節点に頂点を有する多角形M 1およびM 2に切断するとする。 各ノードに対して角度が加えられるので、f(M)= f(M 1)+ f(M 2)となる。 したがって、ピークの式が2つのポリゴンM、M 1、M 2に当てはまる場合、3番目のポリゴンにも当てはまります。
Mが辺を持つ長方形の場合 p そして q格子線に沿って
f(M)=(p - 1)(q - 1)+  = pq。
= pq。
この場合、ピーク式は有効です。 対角線を有する長方形Mを三角形M 1とM 2に切断し、f(M)= f(M 1)+ f(M 2)とf(M 1)= f(M 2)という事実を用いると、ピーク式の妥当性を証明することは容易である。 脚のある直角三角形の場合は、格子の線に沿っています。 長方形からこれらの三角形のいくつかを切り取って、あなたはどんな三角形でも得ることができます。

ピックの公式の証明を完成させるために、任意の多角形を互いに素な対角線で三角形に切り取ることができることに注意してください。
Shの証明
図の領域とこの図に入るノード数との関係は、長方形の場合に特にはっきりと見えます。

みましょう ABCD - ノードに頂点があり、グリッド線に沿って辺がある長方形。
で表す で四角形の内側にあるノードの数 R - 境界上のノード数 グリッドをセルのフロアに移動し、セルの右半分に移動します。

次に、四角形の領域を次のようにノード間で「分散」させることができます。 でノードはオフセットグリッドのセル全体を「制御」します。 R - 4つの境界非コーナーノード - セルの半分、および各コーナーポイント - セルの4分の1。 したがって、長方形Sの面積は次のようになります。

それで、節点と格子線に沿った辺に頂点を持つ長方形のために、我々は公式を確立しました 
この式が長方形だけでなく、グリッドの節点に頂点を持つ任意の多角形にも当てはまることを証明しましょう。
で表す S
メートル
ポリゴンエリアM
頂点を節点とするF
メートル
- 値  どこでで
メートル
- 内部ノード数M、 ある R
メートル
- 境界上のノード数 するとピックの式は次のように書くことができます。
どこでで
メートル
- 内部ノード数M、 ある R
メートル
- 境界上のノード数 するとピックの式は次のように書くことができます。  .
.
式の証明はいくつかのステップに分けられます。
ステップ1
多角形の場合M
グリッドの節点に頂点がある場合は2つの多角形にカットされますM
1
そして M
2
,
グリッドノードにのみ頂点を持つ  。 多角形をしましょうM
ポリゴンにカットM
1
そして M
2
セグメントごとのノードに頂点を持つAB セグメントに属するものを除くすべてのノードAB、
式の左右に同じ寄与を与えます。 セグメントAB上にあるノードを考えます。
。 多角形をしましょうM
ポリゴンにカットM
1
そして M
2
セグメントごとのノードに頂点を持つAB セグメントに属するものを除くすべてのノードAB、
式の左右に同じ寄与を与えます。 セグメントAB上にあるノードを考えます。

そのようなノードがAとBの間にある場合(たとえばC)、多角形の場合M
それは内部的であり、そして多角形のためにM
1
そして M
2
- 境界 したがって、彼の貢献はF
メートル
1に等しく、それぞれの式で  そして
そして  - 0.5では、つまり、そのようなノードの貢献度F
メートル
そして
- 0.5では、つまり、そのようなノードの貢献度F
メートル
そして  等しいです。
等しいです。
ノードAとBを考えてみましょう。 Mそう M 1 , M 2 .
したがって、これらの各ノードの貢献度F
メートル
0.5に等しい  -
単位。 したがって、ノードAとBの合計に対する寄与度は、F
メートル
1に等しい。これは、への寄与より1少ない。
-
単位。 したがって、ノードAとBの合計に対する寄与度は、F
メートル
1に等しい。これは、への寄与より1少ない。  .
しかし
.
しかし  同様に
同様に
全ノードの合計「貢献度」から F メートル 1を引き、から  2を引くと、ノードAとノードBの寄与度の差が補正されます。
2を引くと、ノードAとノードBの寄与度の差が補正されます。
だから  .
.
ステップ2
多角形の場合 Mグリッドノードの頂点が2つのポリゴンに分割されている M 1 そして M 2 (頂点が節点にある場合も)この公式は、2つのポリゴンについて当てはまります。 M、M 1 M 2 それからそれは第3多角形のために本当です。
たとえば、次のようになります。M
1
そして M
2
,
それは  。 それで(最初のステップで),
しかし(によって
最初のステップ)最後の式が等しいF
メートル
,
と平等
。 それで(最初のステップで),
しかし(によって
最初のステップ)最後の式が等しいF
メートル
,
と平等  そしてピック式があります。
そしてピック式があります。
ステップ3
グリッドの節点と頂点がグリッドの線上にある直角三角形のPeak公式を証明しましょう。
三角 ABC 四角形を完成させる ABCD .

長方形の場合、Peakの式は正しいです。 S ABCD = P ABCD . 最初のステップによると F ABCD = P ABC + P ACD 、N ABC = P ACD , だから F ABCD = 2P ABC . しかし S ABCD = 2 S ABC 。 だから S ABC = P ABC .
ステップ4
ピックの式は、グリッドの節点に頂点がある任意の三角形に対して有効です。

絵を考えれば、理解するのは簡単です。グリッド線に沿って走っている辺を持つ特定の長方形からいくつかの長方形を切り取ることによって、そのような三角形を得ることができます。 直角三角形 グリッド線上の足で。 ピークの公式は長方形と直角三角形に当てはまるので(ステップ2を思い出してください)、それは元の三角形にも当てはまります。
多角形をグリッドの節点に頂点を持つ三角形にカットできる場合、Peakの公式がそれに当てはまることを証明しました。
3.タスク
数字の領域を探します。
1
.



![]()
B = 9
G = 4
![]()



![]()
B = 9
G = 5

![]()


![]()
PERVUSHKIN BORISニコラエヴィッチ
CHOU "サンクトペテルブルクスクール" Tet-a-Tet "
最上位の数学教師
檻の中のシートに正方形の部分。 ピックの式!
こんにちは、親愛なる友人たち! 私はあなたがケージの中でシートの上に作られた図形の面積を見つけることができる公式(三角形、正方形、台形、長方形、多角形)についてあなたに話したいです。 これはピックの式です。
彼女は秘密ではありません。 それに関する情報はインターネットで入手可能ですが、この記事の資料は多くの人にとって非常に役に立つでしょう。 この公式は、通常、三角形の面積を求めることに関連して説明されています。 三角形の例では、それを考えます。
USE上にあるタスクには、ケージ内のシート上に構築された多角形が与えられたタスクのグループ全体があり、その領域を見つけることについての質問があります。 細胞の大きさは1平方センチです。
ピカ公式
希望する図の面積は次の式で求められます。

M - 三角形の境界上のノード数(辺と頂点)
N - 三角形の内側のノード数
*「ノード」とは線の交点を意味します。
三角形の面積を求めます。

ノードに注意してください。

1セル= 1 cm
M = 15(赤で表示)
N = 34(青い印)

別の例 平行四辺形の面積を求めます。

ノードに注意してください。

M = 18(赤で表示)
N = 20(青い印)

台形の面積を求めます。

ノードに注意してください。

M = 24(赤で表示)
N = 25(青い印)

多角形の面積を求めます。

ノードに注意してください。

M = 14(赤で表示)
N = 43(青い印)

これらの図の面積の対応する公式によって台形、平行四辺形、三角形の面積を見つけることがより簡単でより速いことは明らかです。 しかし、あなたはこの方法でそれができることを知っています。
しかし、5つ以上の角度を持つ多角形が与えられるとき、この公式はうまくいきます。
次の図を見てください。

これらは典型的な数字です、タスクで彼らの領域を見つけることについての質問があります。 そのようなものまたはそれらに類似したものが試験にかけられます。 ピーク式を使用すると、このような問題は1分で解決されます。 たとえば、図形の面積を見つけます。

ノードに注意してください。

M = 11(赤で表示)
N = 5(青い印)


解決策を見る
ケージサイズが1 cm 1 cmの市松模様の紙に描かれた四角形の面積を求め、その答えを平方センチメートルで与えます。

解決策を見る
ケージサイズが1 cm 1 cmの市松模様の紙に描かれた四角形の面積を求め、その答えを平方センチメートルで与えます。
解決策を見る
ケージサイズが1 cm 1 cmの市松模様の紙に描かれた四角形の面積を求め、その答えを平方センチメートルで与えます。
解決策を見る
もちろん、これらの「マイクロフィギュア」をもっと単純な形(三角形、台形)に分割することも可能です。 あなたが決める方法。
記事で指定されているアプローチを検討してください。」 四辺形の面積。 普遍的な方法".
図の領域を見つけます。
その近くに長方形を記述します。
四角形の面積(この場合は四角形)から、得られた単純な図形の面積を差し引きます。
プレゼンテーションプレビューを使用するには、自分用のGoogleアカウント(アカウント)を作成してログインします。https://accounts.google.com
スライドのキャプション:
中学校№78 "A"クラスの完成した学生Yunosheva Xenia講師:Babina Natalia Alekseevna Salsk 2011式ピカ年
作品の目的:学校のカリキュラムとは異なる、異なる存在の明確化、格子多角形の面積を見つけるための公式。 目的の式の範囲
はじめに 一般教育学校で受けられる数学教育は、一般教育と現代人の一般文化の不可欠な要素です。 この段階では、学校制度は11年間の勉強のために設計されています。 11年生の終わりにすべての学生は統一州試験に合格する必要があります。これは学校での勉強中に得られた知識のレベルを示します。 しかし、学校のプログラムは常に問題を解決するための最も合理的な方法を提供するわけではありません。 たとえば、2010年の試験の結果を見ると、多くの学生が課題B6のためにポイントを失うことは明らかです。 私は時間を節約し、このタスクを正しく解決する方法に目標を設定しました。
タスクB6。 大きさが1 cm x 1 cmのセルを持つ市松模様の紙の上に、数字が示されています(図を参照)。 面積を平方センチメートルで見つけてください。
それで、この課題を解決するために、私たちがグレード8で勉強する領域を見つけるために公式を適用する必要があります。しかし、これは多くの時間がかかるでしょう。 それゆえ、研究を行った後、私はピーク定理があることを発見しました。それは学校のカリキュラムでは研究されていませんが、それは私がより早く課題に対処するのを助けるでしょう。
歴史的背景 Georg Alexander Pick(1859年8月10日 - 1942年7月26日)はオーストリアの数学者でした。 彼はテレジン強制収容所で亡くなりました。 今日では、ポリゴングリッドの面積を決定するためのピック式によって知られています。 彼は1899年にHugo Steinhausが1969年版の数学的画像にそれを含めたときに一般的になった記事で彼の式を発表した。 ピークはウィーン大学で学び、1880年に博士号を擁護しました。 博士号を取得後、プラハのSherlsko-Ferdinand大学のアーネストマッハ助教授に就任。 彼は1881年にそこで教師になりました。 1884年に大学を卒業し、ライプツィヒ大学でFelix Kleinと仕事を始めました。 彼は1927年に引退するまでプラハに留まり、その後ウィーンに戻った。 ピークは1911年に数理物理学科の教授としてアルバートアインシュタインを任命したプラハの(当時)ドイツの大学で委員会を率いた。 ピークはチェコ芸術科学アカデミーのメンバーに選出されたが、ナチスがプラハを占領した後追放された。 1927年に引退した後、ピークは彼が生まれた都市ウィーンに戻りました。 Anschlussの後、1938年3月12日にナチスがオーストリアに入ったとき、ピークはプラハに戻った。 1939年3月、ナチスはチェコスロバキアを侵略した。 ジョージは1942年7月13日にテレジン強制収容所に送られました。彼は2週間後に亡くなりました。
ピックの定理 ピックの定理は、組み合わせ幾何学と数の幾何学の古典的な結果です。 整数の頂点を持つ多角形の面積は、Â+Г/ 2 - 1の合計に等しくなります。ここで、Âは多角形の内側の整数点の数、Гは多角形の境界上の整数点の数です。
ピックの定理の平坦性を証明する。 このような多角形は、格子節点に頂点がある三角形に分割するのが簡単で、内側にも側面にも節点がありません。 これら全ての三角形の面積は同じであり、1 / 2に等しいこと、従って多角形の面積はそれらの数Tの半分に等しいことを示すことができる。この数を見出すために、多角形の辺の数をnで表す。 頂点を含む、辺のノード数 すべての三角形の角度の合計はπТです。 今、私たちは別の方法でこの量を見つけるでしょう。 任意の内部ノードにおける頂点との角度の合計は2πであり、すなわちそのような角度の合計は2π iである。 辺ではなく辺の節点での角度の合計は(b - n)πで、多角形の頂点での角度の合計は(n - 2)πです。 したがって、πT = 2iπ+(b - n)π+(n - 2)πとなり、ピーク式として知られる多角形の面積Sの式が得られます。 たとえば、図ではb = 9、i = 24であるため、多角形の面積は27.5です。
アプリケーション タスクB6に戻ります。 今、新しい式を知って、私たちは簡単にこの四角形の領域を見つけることができます。 Bは5なので。 G - 14、それから5 + 14:2-1 = 11(cm 2)この四辺形の面積は11 cm 2です。
同じ式で、三角形の面積を求めることができます。 B-14、G-10、それから14 + 10:2-1 = 18(cm 2)なので、この三角形の面積は18 cm 2です。
B-9、G-12の場合:9 + 12:2-1 = 14(cm 2)この四辺形の面積は14 cm 2です。
式の範囲 この式がさまざまな種類の試験や課題などで使用されているという事実に加えて、この式は私たちの周りの世界全体に付随しています。
ピックの式によると、S = B + 1/2 D-1 1)胴体B = 9、D = 26、S = 9 + 1/2・26 - 1 = 9 + 13 - 1 = 21 2)尾B = 0、D = 8、 S = 0 + 1 / 2・8 −1 = 3 3)S = 21 + 3 = 24
ピックの式によると、S = B + 1/2 D -1 B = 36、D = 21 S = 36 + 1/2・21 -1 = 36 + 10.5-1 = 45.5
結論 その結果、学校カリキュラムで研究されていない地域を見つけるという問題を解決するためのさまざまな方法があるという結論に至り、それらをピーク式の例を使って示しました。
ハンドブック 自己交差のない多角形は、そのすべての頂点が整数座標(直交座標系)の点にある場合、ラティスと呼ばれます。 座標平面上の点は、その座標が両方とも整数の場合は整数と呼ばれます。
「問題解決は、
水泳、スキー、ピアノの演奏
あなたは善を模倣することによってのみそれを学ぶことができます
サンプルと常に練習」
(D.ポヤ)

オーストリアの数学者、
ユダヤ人の家族に生まれました。
マザージョセフシュライジング、
父アドルフジョセフPik。
ジョージピーク
10.08.1859 - 13.07.1942

履歴書
ジョージアレクサンダーピーク
だった 才能のある子、私立の機関を率いる父親を教えた。 16歳の時、ジョージは高校を卒業し、ウィーン大学に入学しました。 20年で、物理学と数学を教える権利を受けました。 1880年4月16日、LeoKönigsbergerの指導の下、Peakは博士論文「Abelian積分のクラスについて」を擁護した。 1888年にプラハのドイツ大学で、ピークは数学の特別教授の地位を与えられ、その後1892年に彼は普通の教授になりました。 19001901年に彼は哲学部の学部長を務めました。 彼の名前はPick行列、Pick Nevanlinna内挿、Schwartz Pick補題に関連付けられています。 1942年7月13日、ピークはボヘミア北部のナチスによって作られたテレジエンシュタット収容所に強制送還され、そこで2週間後に82歳で亡くなりました。

ジョージアレクサンドロフピーク
1899年に式を発見
S = B + R /2-1
Sは多角形の面積 ,
G - グリッド内のノード数
B - グリッドノード数



S = 15 - 3 - 3 - 5/2 = 6.5 S = 6 + 3 / 2-1 = 6.5


S = 20 - 2 - 3 - 1 - 3/2 - 5/2 = 10 S = 9 + 4/2 - 1 = 10

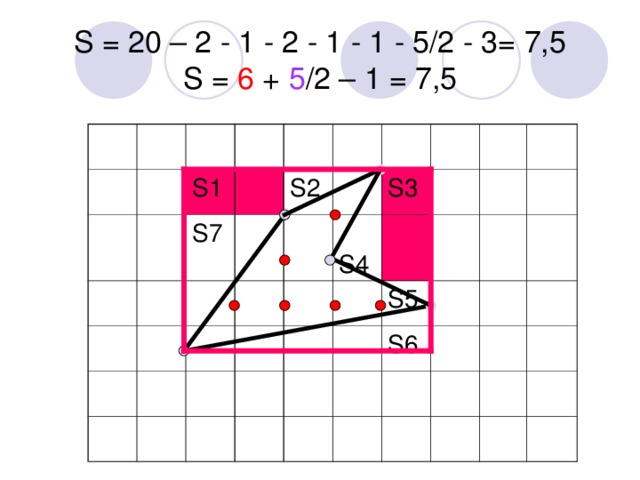
S = 20 - 2 - 1 - 2 - 1 - 1/5/2 - 3 = 7.5 S = 6 + 5/2 - 1 = 7.5


台形ABCDの面積を求める
G = 10、B = 5、
= B + D / 2 - 1 = 5 + 10/2 - 1 = 9

四角形ABCDの面積を求めます。
正方形のセルの辺が1であると仮定します。
G = 6、B = 8、
S = B + D / 2 - 1 = 8 + 6/2 - 1 = 10

ダイヤモンドABCDの面積を求める
正方形のセルの辺が1であると仮定します。
G = 4、B = 7、
S = B + D / 2 - 1 = 7 + 4 / 2-1 = 8

1cm×1cmの大きさのセルを有する市松模様の紙は三角形(台形)を描く(図参照)。
面積を平方センチメートルで見つける:

図の面積、
ピーク式を使用して計算
図の面積に等しい
幾何学の公式によって計算されます。
市松模様の紙の上の図形の問題では、ノードはセルの角です。